Contents
Introduction
Waves are extremely important in physics as they form the foundation of a wide range of topics, from simple mechanical waves on a string to the use of optics in astrophysics.
In this post, we’re going to have a tour of the key principles of waves to understand the essentials of this important topic.
Let’s begin!
What is a wave?
A wave is a transfer of energy through a medium by means of oscillations. When part of the medium oscillates, it causes the next part to oscillate, thereby creating a propagation that carries energy in the wave direction.
There are two types of media that can carry waves: materials and fields. For example, sound travels through air by the oscillation of gas molecules, while electromagnetic waves travel by the oscillation of an electromagnetic field.
Waves that travel through fields do not require a material medium to propagate. As a result, they can travel through a vacuum and, in fact, passing through a material slows them down.
Wave properties
All waves have some basic properties in common. For example, the following graph represents a snapshot of a wave at a particular time as it travels to the right.
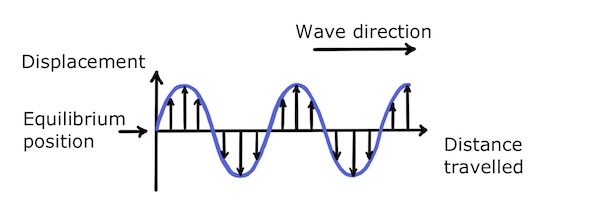
The \(y\)-axis represents the displacement of an oscillating point on the wave and the \(x\)-axis represents the distance in the wave direction. Progression of the wave can be seen by comparing this graph to a slightly later snapshot where we can see that the wave has travelled forwards slightly:

Two key properties of the wave are its amplitude and wavelength. Amplitude is the maximum displacement of an oscillating point and wavelength is the distance between two points separated by a whole wave cycle.

Crests and troughs are the points of highest and lowest displacements. The phase of a point on the wave is how far through a full cycle or oscillation that point is at a given time. Phase is measured in the same units as angles since a full cycle is analogous to \(360^{\circ}\) or \(2\pi\).
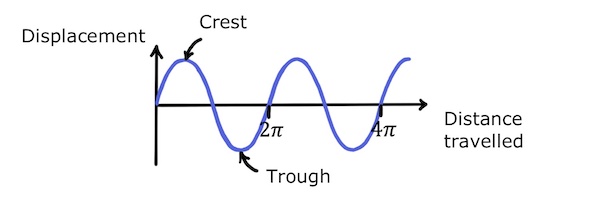
Finally, the time taken for a point on the wave to complete a full oscillation is the period, \(T\). This is the inverse of frequency, \(f\), which is the number of wave cycles to pass a given point per second:
\(f=\frac{1}{T}\)
The wave equation
We can use the familiar
\(speed=\frac{distance}{time}\)
to work out the speed, \(v\), of a travelling wave. We know the wave travels a distance of one wavelength, \(\lambda\), during the time taken for a complete cycle, so:
\(v=\frac{\lambda}{T}\)
But since \(f=\frac{1}{T}\), we have:
\(v=f\lambda\)
This is the wave equation for calculating the speed of a wave!
Transverse waves
A transverse wave is a wave in which the oscillations of the carrying medium are perpendicular to the wave direction.
For example, in a wiggling rope the rope oscillates up and down while the wave travels from left to right:
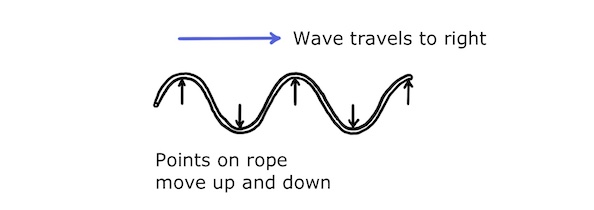
This looks a lot like the displacement-distance graphs above. That’s because the displacements of the points on the rope are perpendicular to the direction of travel, just like the perpendicular axes on the graph.
Other examples of transverse waves include electromagnetic waves and S-waves in earthquakes.
Longitudinal waves
A longitudinal wave is a wave in which the oscillations of the carrying medium are parallel to the wave direction.
The most common example is sound which propagates by air oscillating back and forth in the wave direction.
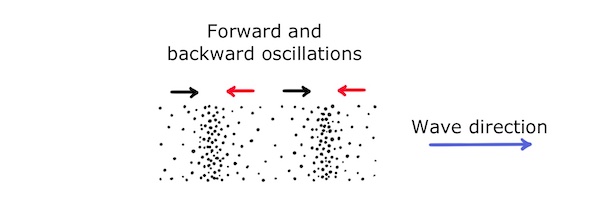
These oscillations create areas of compression (high pressure) and rarefaction (low pressure) in the air:
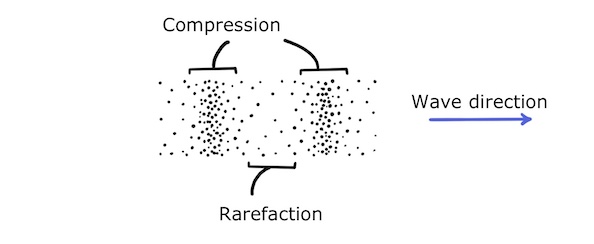
We can see that the wavelength of the sound is the distance between two points separated by a whole cycle:

Gas molecules in the air that have oscillated forwards have a positive displacement and gas molecules that have oscillated backwards have a negative displacement. Between these areas of positive and negative displacement there are points of zero displacement, where the gas molecules are in their equilibrium position.
We can match up the areas of positive and negative displacement with the familiar graph that we saw above.
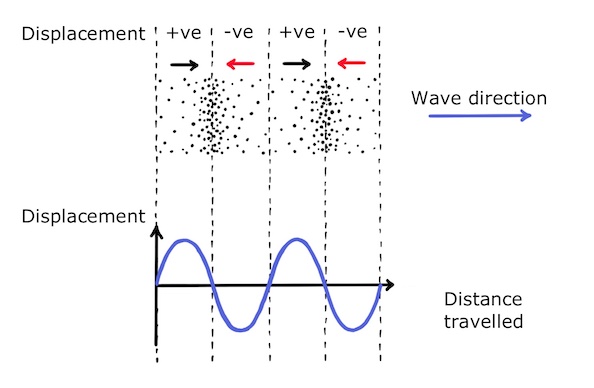
In this way, the displacement-distance graph that we saw above can also represent a longitudinal wave.
Diffraction through a gap
All waves exhibit a special behaviour called diffraction when they meet the edge of a barrier. As the wave passes the edge, its energy spreads out around the barrier causing the wavefronts to bend.

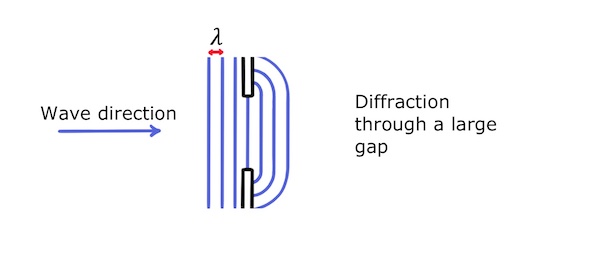
When two barriers form a gap, there is diffraction at each edge. The wavefronts that pass through the gap are undisturbed in the middle and curved at the ends.
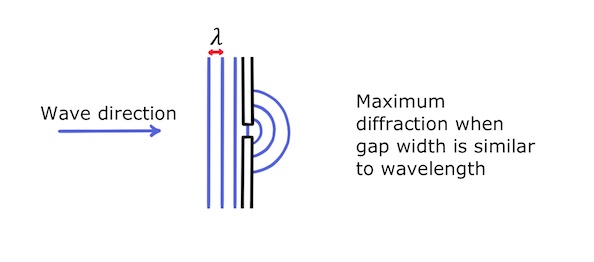
Maximum diffraction occurs when the gap width is equal to the wavelength:
For tiny gaps that are much smaller than the wavelength, hardly any wave energy gets through the gap and the wave is mostly reflected backwards. By contrast, for very large gaps the majority of the wave passes through undisturbed.
Refraction at a boundary
Another important behaviour of waves is that they change direction when they pass through a boundary between two media if they approach the boundary at an angle to the normal. This is called refraction and it happens because the speed of the wave changes when it enters the new medium.
For example, when light travels from a less optically dense material to a more optically dense material, it slows down. This causes its wavefronts to change orientation, bringing the ray closer to the normal:
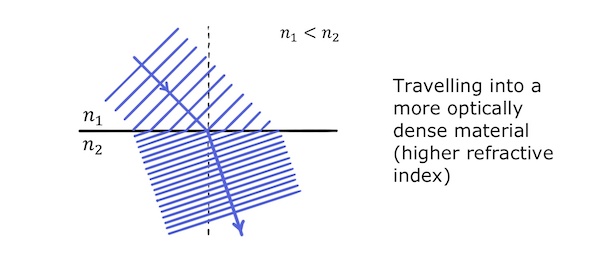
Conversely, when light travels from a more optically dense material to a less optically dense material, it speeds up, bending the ray away from the normal:
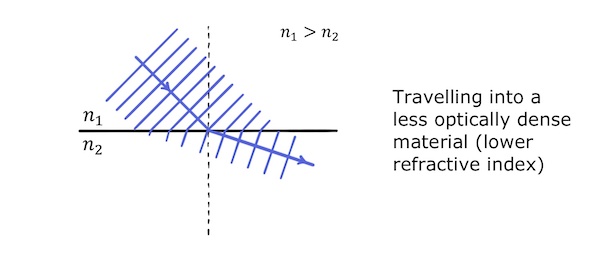
The optical density of a material is defined by its refractive index, \(n\), which is the speed of light in a vacuum, \(c\), divided by the speed of light in the material, \(c_m\):
\(n=\frac{c}{c_m}\)
Since this is the ratio of two speeds, the refractive index has no units.
We can label the above diagram of travelling into a less optically dense material with the angle of incidence, \(\theta_1\), the angle of refraction, \(\theta_2\), and the refractive indices, \(n_1\) and \(n_2\), of the two materials:
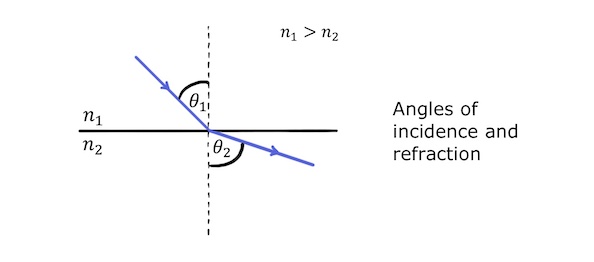
The relationship between these quantities is provided by Snell’s law:
\(n_1sin\theta_1=n_2sin\theta_2\)
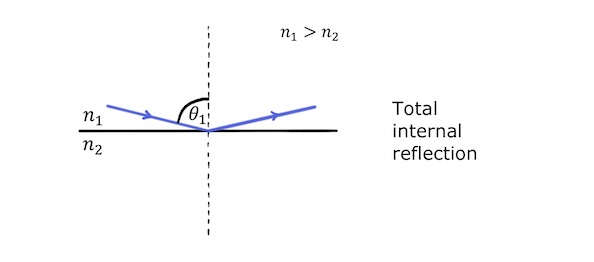
In the special case of light travelling from a more optically dense material to a less optically dense material (\(n_1>n_2\)), the angle of incidence can be increased until the angle of refraction is \(90^{\circ}\):
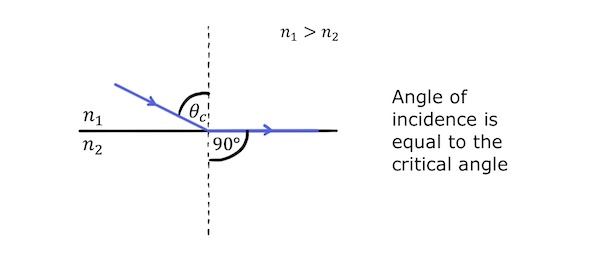
At this point, the angle of incidence is equal to the critical angle, \(\theta_c\), which represents a limit of refraction. For angles of incidence greater than the critical angle, there is no further refraction and all the light is reflected. This is called total internal reflection.
Principle of superposition
Waves don’t always travel in isolation. Sometimes they meet and interfere! This means they superimpose to form a resultant wave.
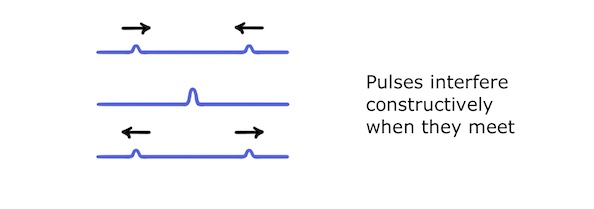
Two identical pulses travelling towards each other will interfere constructively to form a combined pulse with a larger amplitude:
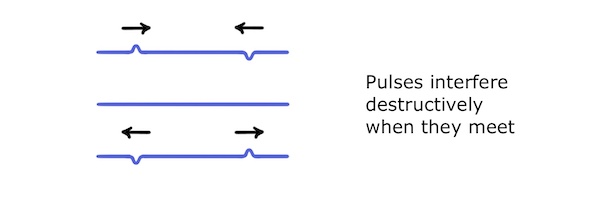
If, however, the second pulse has a negative amplitude, they will interfere destructively and cancel each other out when they meet:
Continuous waves travelling in opposite directions can also interfere with each other. When they are in phase, they interfere constructively:

And when they are out of phase, they interfere destructively:

Interference patterns
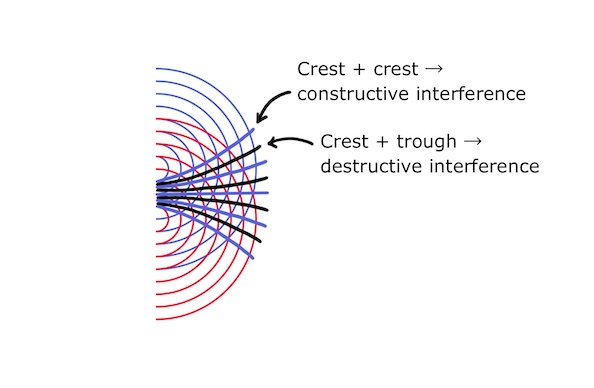
We can apply these principles to more complex scenarios such as the interference of circular wavefronts.

Where crests meet crests, there is constructive interference and the resulting wave has a combined amplitude. Where crests meet troughs, there is destructive interference and if the circular waves have the same amplitude they will cancel each other out.
This sets up lines of constructive and destructive interference:
If the waves are light waves, a screen will show bright and dark fringes coinciding with the lines of constructive and destructive interference:

The intensity on the screen peaks at a central maximum (of “order” zero) and smaller maxima (of first, second order, etc) result from the surrounding bright fringes.

Conclusion
Phew, what a tour of waves! With this strong foundation in the behaviour of waves, you are in an excellent position to start practicing waves questions or tackle more advanced topics such as standing waves, polarisation of light, and diffraction gratings.
I hope you enjoyed learning all about waves. Happy studying!
