Particles & the Standard Model for A Level Physics

Introduction

Particle physics is one of my favourite topics in A Level physics! It opens up the world of the very small and introduces us to the fundamental building blocks of our universe.

In this post, I’m going to take you through the Standard Model of particle physics, the particles that belong to it, and how they are classified.

Let’s begin!

What is the Standard Model of particle physics?

The Standard Model of particle physics is our description of the elementary particles in the universe, how they combine to form composite particles, and how they interact with each other through the four fundamental forces.

Elementary particles of the Standard Model

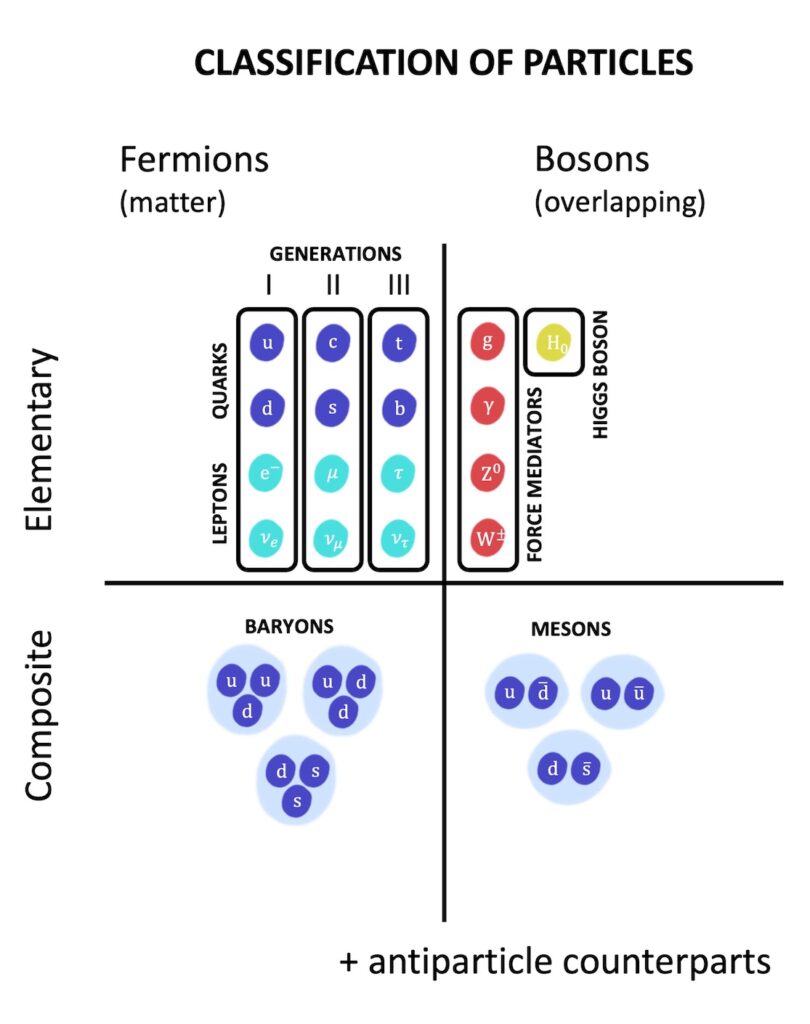
According to the Standard Model, the basic building blocks are the elementary particles. These are grouped into three families: the quarks, the leptons, and the elementary bosons which can be divided into the force carrying bosons and the Higgs boson.

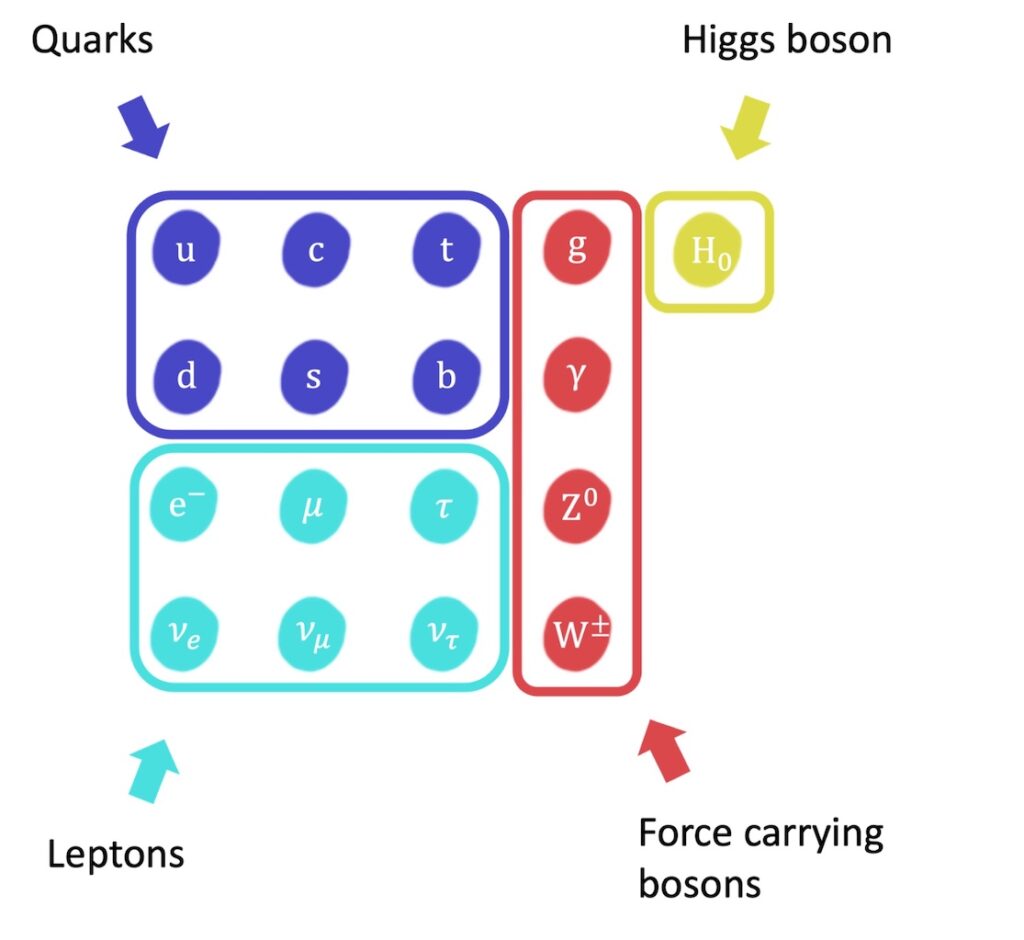
Quarks and leptons are important in everyday matter because neutrons and protons in the atomic nucleus are made from quarks, and the electron is a member of the lepton family.

Meanwhile, the force carrying bosons are involved in the mechanism of the four fundamental forces. According to this mechanism, particles exchange force carrying bosons in order to exert forces on each other. The role of the Higgs boson is more mysterious, but it is thought to be responsible for giving many particles their mass.

What are antiparticles?

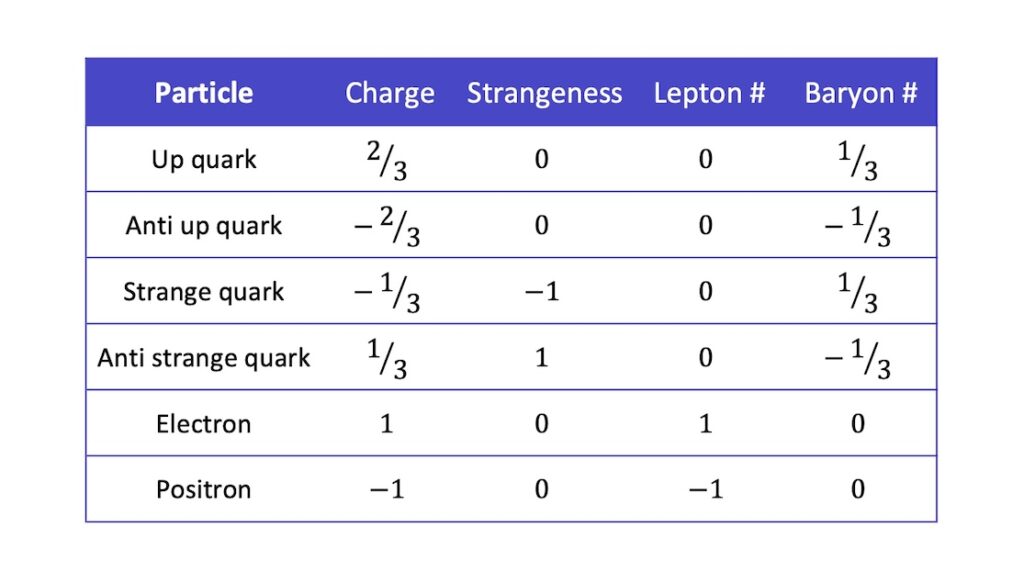
In the Standard Model, each particle has an antiparticle. Antiparticles are the same as their particle counterparts, except they have opposite charge, strangeness, lepton number and baryon number.

(Strangeness is defined as \(-1\) for the strange quark and \(0\) for all other elementary particles; lepton number is defined as \(1\) for each lepton and \(0\) for all other elementary particles; baryon number is defined below.)

For example, the up quark has a charge of \(2 \big/ 3\) and a baryon number of \(1 \big/ 3\), so its antiparticle has a charge of \(-2 \big/ 3\) and a baryon number of \(-1 \big/ 3\). We can see the opposite values of charge, strangeness, lepton number and baryon number for the following particles and their antiparticles:

It is a curious fact that some elementary particles have values of zero for all these properties. As a result, they are the same as their antiparticle (antiparticle = self). For example, the Higgs boson is its own antiparticle:

In terms of nomenclature, most antiparticles are denoted with a bar above the particle symbol. For example:

Up quark: \(\mathrm{u}\)
Antiup quark: \(\mathrm{\overline{u}}\)

However, some antiparticles have their own special symbols, like the positron, the electron’s antiparticle:

Electron: \(\mathrm{e^-}\)
Positron: \(\mathrm{e^+}\)

While antiparticles exist naturally in the universe, they do not naturally combine to form antiatoms and are far outweighed by their particle counterparts. The question of why matter dominates over antimatter in the universe is a deep, unanswered question in physics.

Composite particles: hadrons

Quarks can combine to form quark composites which are called hadrons, and these fall into two groups: baryons and mesons. Baryons are made from three quarks and mesons are made from a quark and an antiquark:

Baryons: \(\mathrm{qqq}\)
Mesons: \(\mathrm{q\overline{q}}\)

For example, the familiar proton of the atomic nucleus is a baryon with a quark constitution of two up quarks and a down quark (\(\mathrm{uud}\)). The Pi-plus particle is a meson comprising an up quark and an antidown quark (\(\mathrm{u\overline{d}}\)).

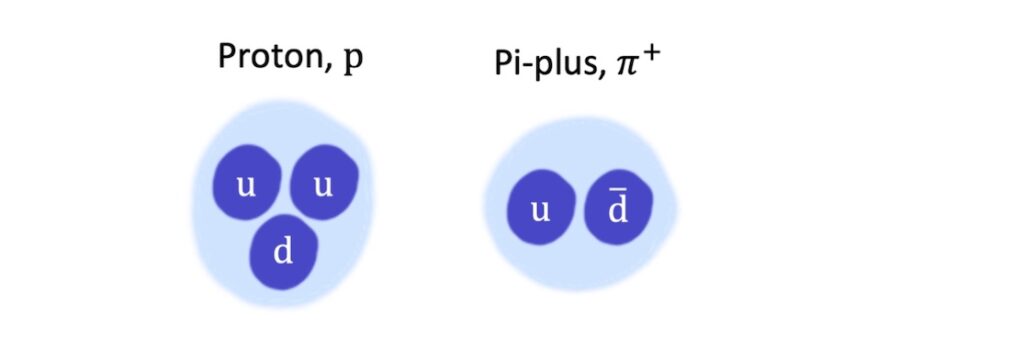
The neutron of the atomic nucleus is also a baryon, so baryons play an important role in everyday matter. Mesons, by contrast, are not matter particles at all, as we will see below.

Baryon number, which we encountered above, is defined as \(1\) for baryons and \(1 \big/ 3\) for quarks (and therefore \(-1\) for antibaryons and \(-1 \big/ 3\) for antiquarks). Since mesons each contain a quark and an antiquark, they have a baryon number of \(0\).

Fermions and bosons

A very important distinction for all particles, whether elementary or composite, is whether they are fermions or bosons.

Fermions are particles with half-integral spin (e.g. \(1 \big /2\), \(3 \big /2\),…)
Bosons are particles with integral spin (e.g. spin \(0\), \(1\), etc)

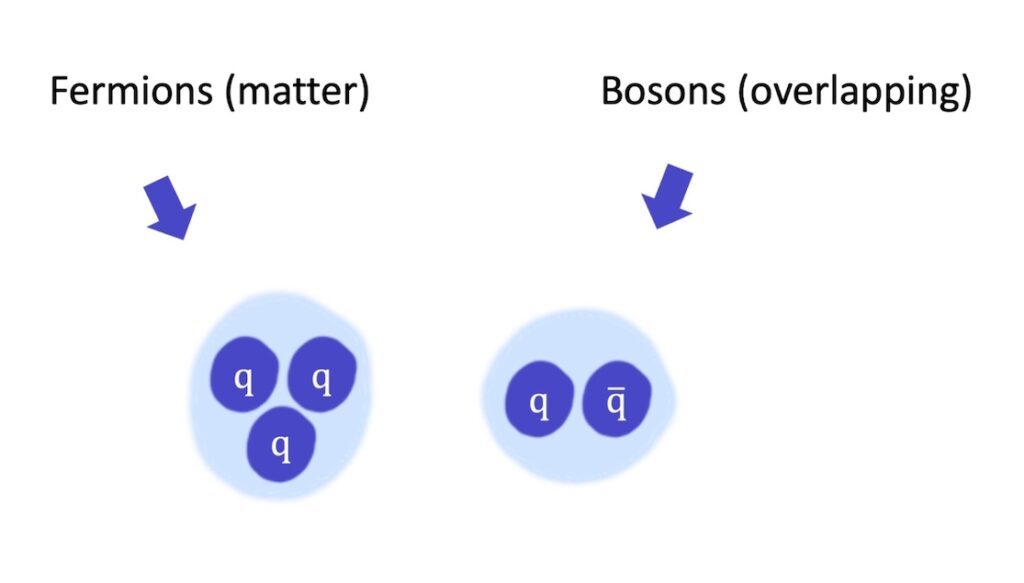
Fermions fully occupy their own space and cannot be in the same place at the same time. By contrast, bosons can overlap with each other and occupy the same space.

Consequently, fermions are matter particles and bosons are not matter particles. (To remember this, you can think “fermions are firm!”)

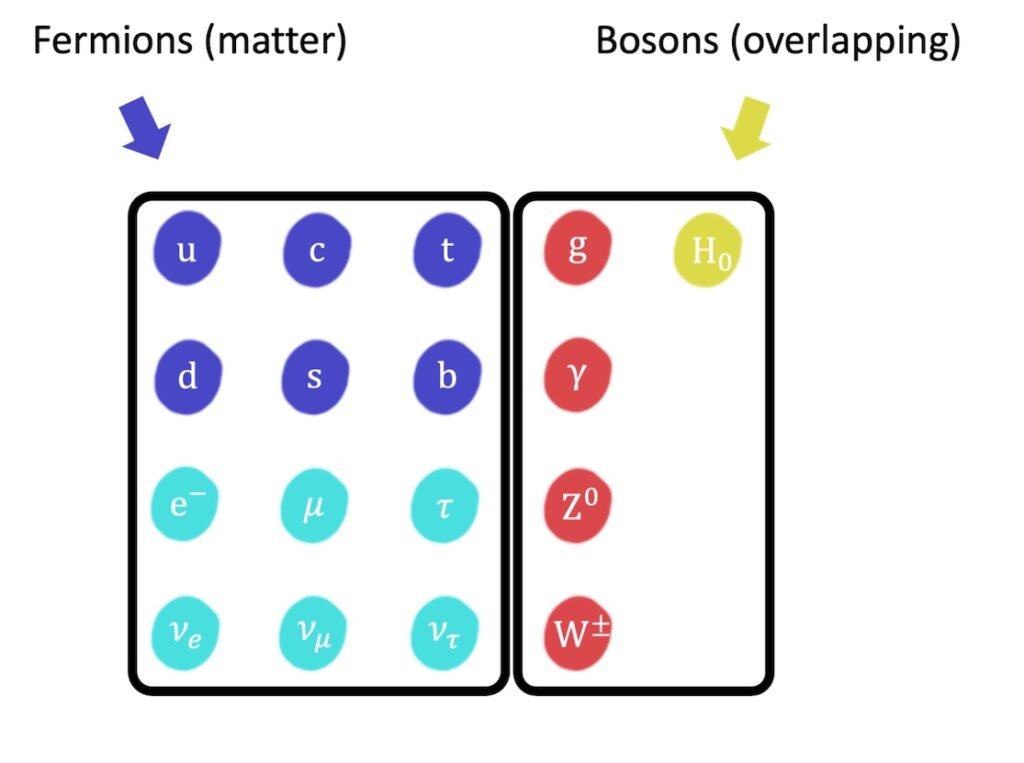
For example, quarks and leptons have half integral spin and the force carriers and the Higgs particle have integral spin:

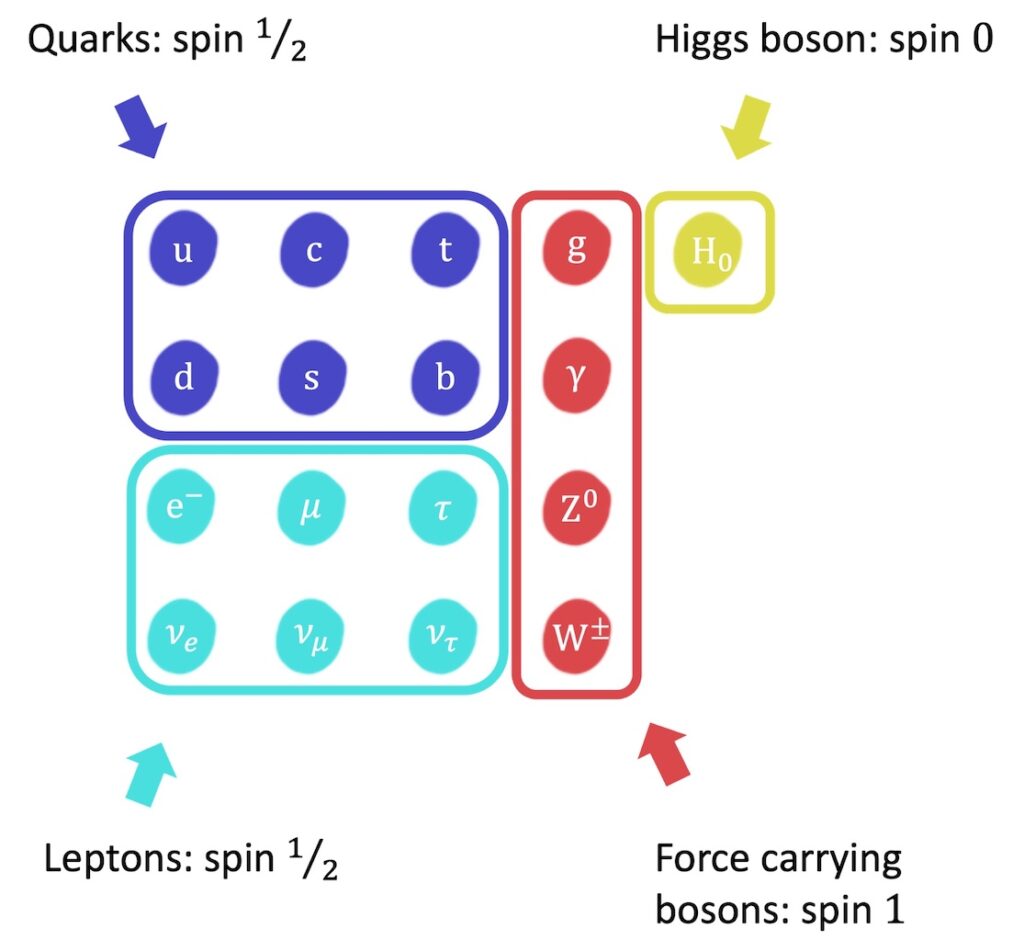
So quarks and leptons are fermions and the force carriers and the Higgs particle are bosons:

The same applies to composite particles. Baryons have half integral spin and mesons have integral spin:

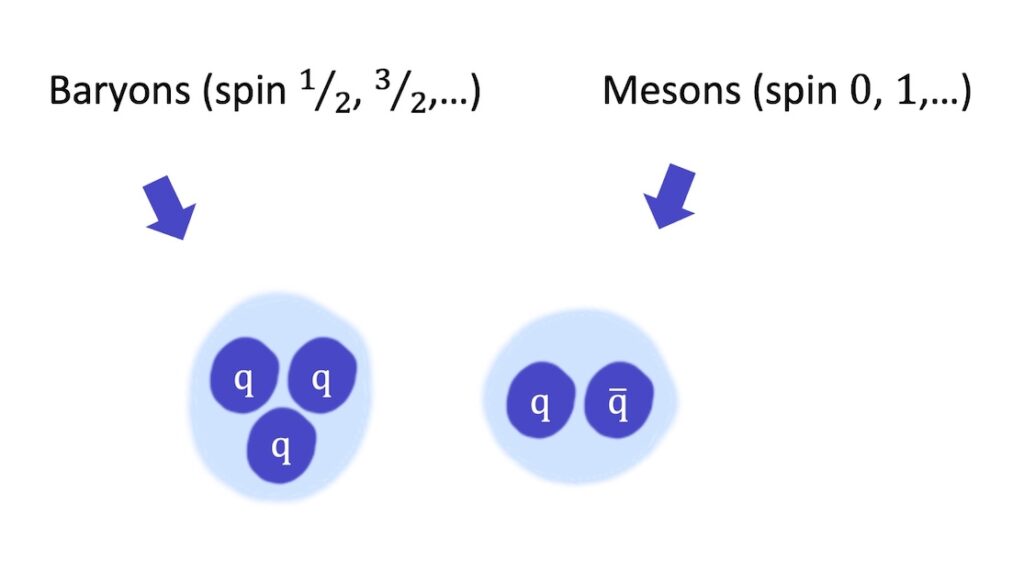
So baryons are fermions and mesons are bosons:

The key distinctions between fermions and bosons are summarised as follows:

A word of warning: do not get confused between having a mass and being a matter particle. All fermions and most bosons have a mass, but only fermions (which have half integral spin and fully occupy space) are matter particles.

Three generations of matter

The elementary matter particles (quarks and leptons) can be categorised into generations according to their mass.

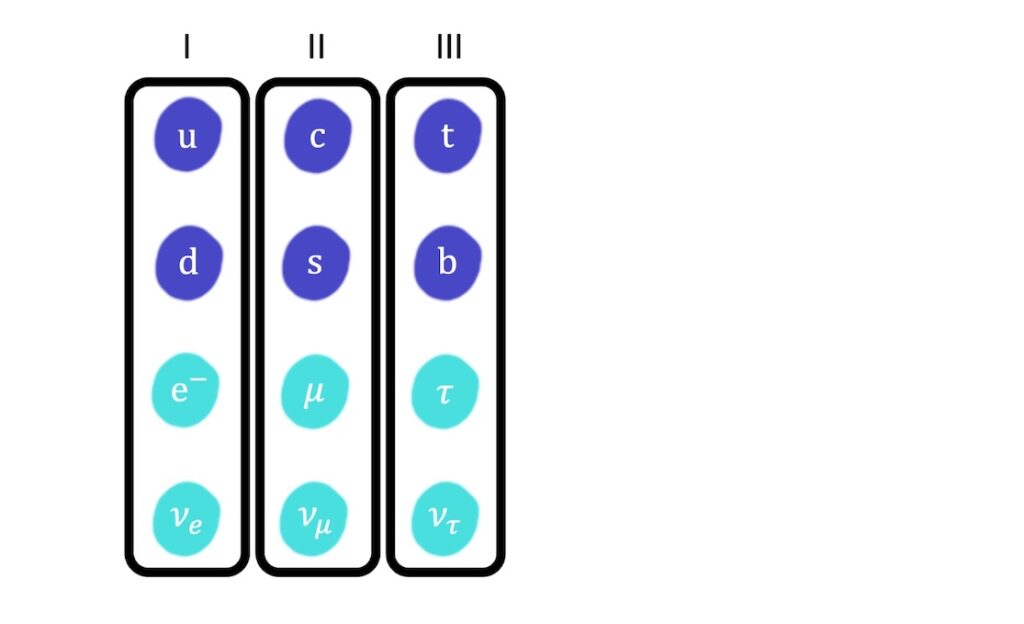
With each increasing generation, each particle is heavier than its counterpart particle in the previous generation.

It is interesting to note that the first generation contains all the elementary particles making up everyday matter. This is because lighter particles are more stable than their heavier counterparts which decay rapidly and only exist in very high energy environments.

Classification of particles

In this post, we have seen that particles can be classified according to whether they are:

Bringing all this together, we can zoom out and see how the particles of the Standard Model fit together in this classification scheme:

Conclusion

I hope you’ve enjoyed this review of the Standard Model of particle physics! This is a super fun topic and provides the perfect springboard for exploring in more detail the properties and roles of the elementary and composite particles.

Happy studying!