Contents
Introduction
A resultant force on an object can cause it to move forwards and accelerate, but forces on objects can also cause them to rotate.
In this blog post, we will explore how forces can have a turning effect, and consider concepts such as object stability and rotational equilibrium.
Let’s begin!
What is a moment of a force?
A moment of a force is a turning effect that causes an object to rotate about an axis of rotation.
It is equal to the magnitude of the force \(F\) multiplied by the perpendicular distance \(x\) between the line of action of the force and the axis of rotation.
\(Moment=Fx\)
For example, imagine a circular object that is pivoted at its centre and experiences a force \(F\) at a perpendicular distance of \(x\) from the pivot. It will experience a moment of \(Fx\) that creates a turning effect, in this case in the clockwise direction:
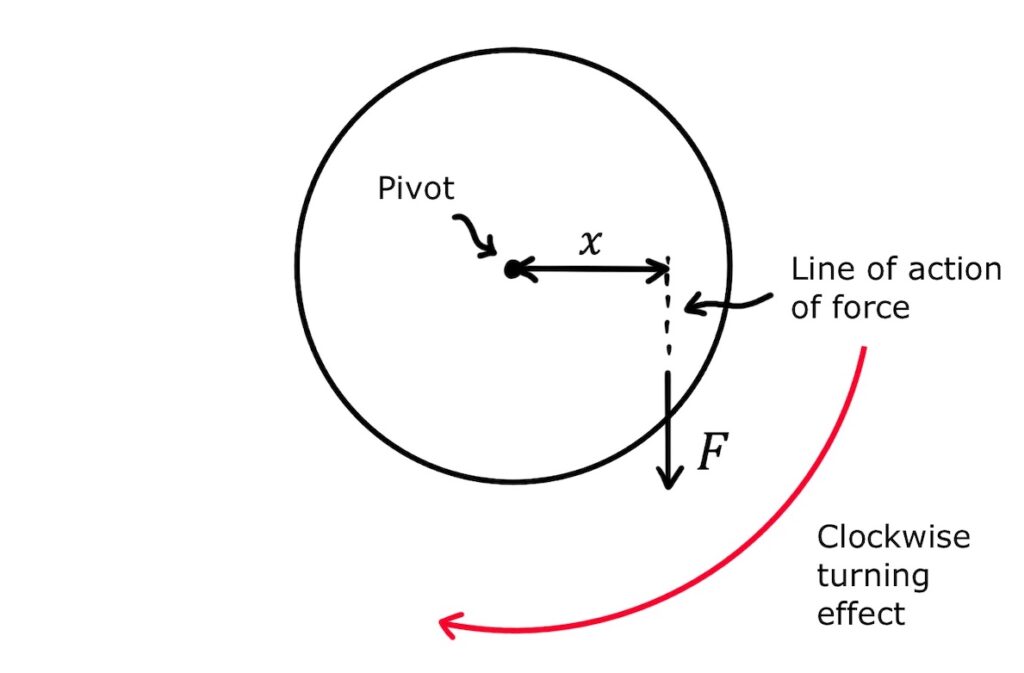
It’s worth noting that since moments have a direction (clockwise or anticlockwise), they are vectors, not scalars.
Object stability and toppling
Moments can be used to explain whether an object on a surface is stable or whether it will topple over.
For example, a vehicle resting on its right wheels is subject to a moment caused by its own weight acting through its centre of gravity.

In the first position, the line of action of the vehicle’s weight is inside the vehicle’s base area. The moment therefore has an anticlockwise turning effect and causes the vehicle to rotate back onto its four wheels.
In the second position, the line of action of the vehicle’s weight is outside its base area. The moment consequently has a clockwise turning effect and causes the vehicle to rotate onto its side (i.e. topple over).
The higher the centre of gravity and the smaller the base area, the less stable the object will be. To increase stability, a vehicle requires a low centre of gravity and a wide base area.
Rotational equilibrium and the principle of moments
The principle of moments states that if the sum of the clockwise moments about a point on an object is equal to the sum of the anticlockwise moments about the same point, then the object will be in rotational equilibrium.
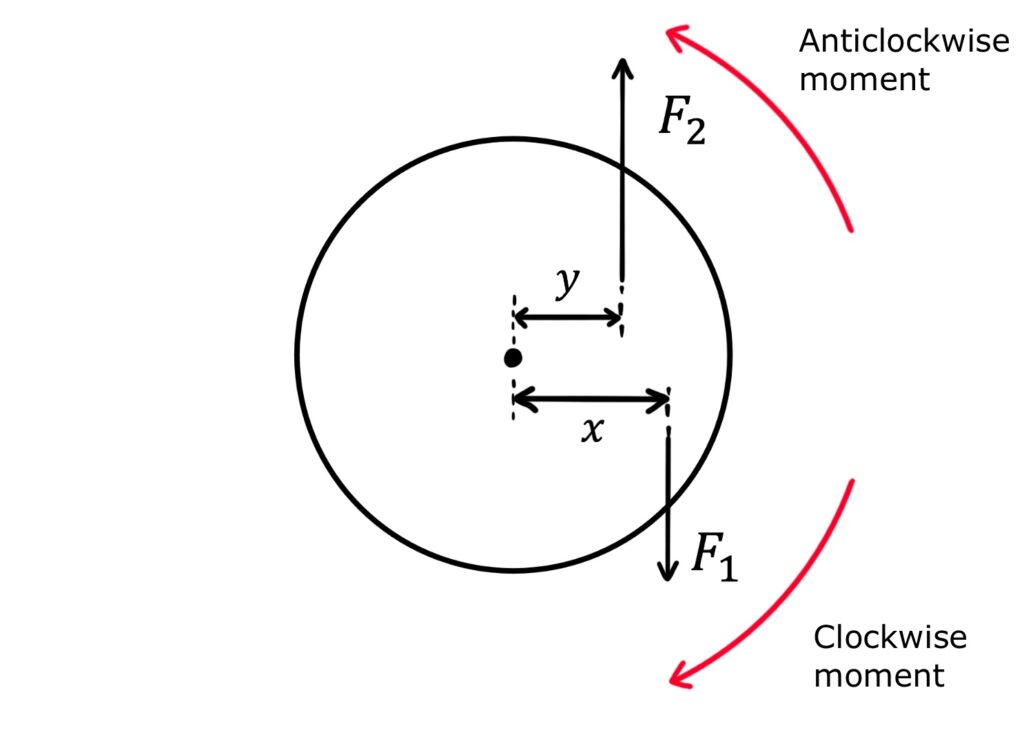
For example, a centrally pivoted object subject to a clockwise moment \(F_1x\) and an anticlockwise moment \(F_2y\) will be in rotational equilibrium if \(F_1x=F_2y\):

Here’s a similar example of rotational equilibrium when \(F_1x=F_2y\):
In another example, a plank rests on a pivot and a load of weight \(W_1\) is placed on the plank to keep it balanced. The plank has a weight of \(W_2\).
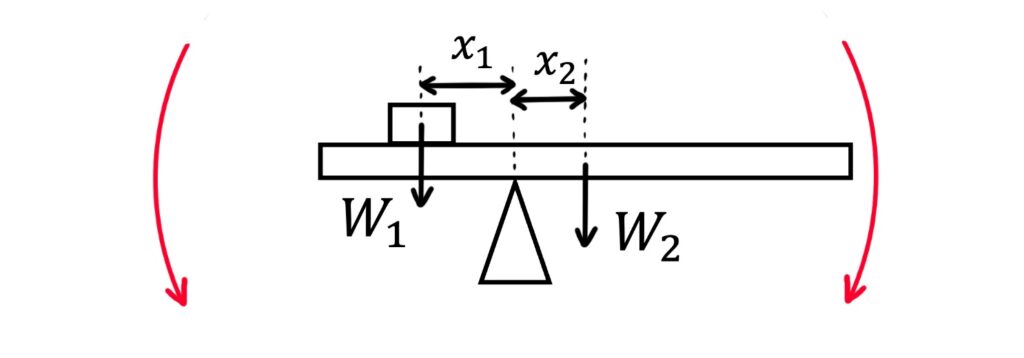
The system is in rotational equilibrium when \(W_1x_1=W_2x_2\).
Finding the centre of gravity of an irregular object
We have seen on a few occasions that an object’s weight acts through its centre of gravity.
For a regular object such as a circular object, the centre of gravity is at the centre of the object. But how can we find the centre of gravity of an irregular object?
Here are two simple methods.
In a first method, we can hang an irregular object from a point A, and also hang a string with a weight on the end from the same place. We can then draw a line on the object along the string.
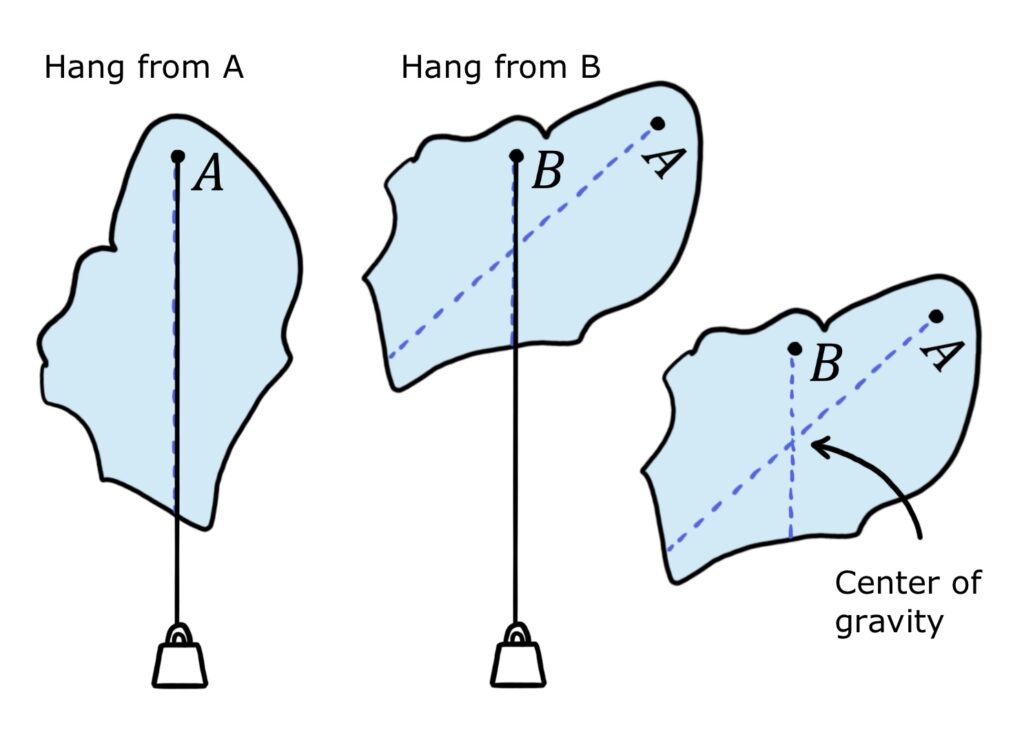
We then rotate the object and hang it from a different point B, and draw a new line. The point where the lines cross is the centre of gravity.
In another method, we can place an irregular object of mass \(M\) on a pivot. At one end of the object, we attach a small load of mass \(m\).
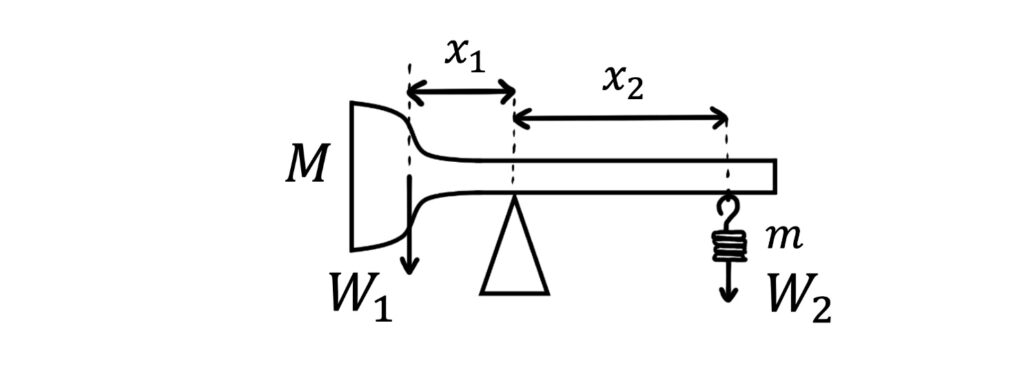
Initially, the anticlockwise moment from the mass of the object is greater than the clockwise moment from the small load and the system is unbalanced. However, we can increase the load \(m\) until the system is in rotational equilibrium, at which point the moment caused by the object’s weight is equal to the moment caused by the small load:
\(W_1x_1=W_2x_2\)
\(\implies Mgx_1=mgx_2\)
Cancelling \(g\) and rearranging for \(x_1\) gives:
\(x_1=\frac{mx_2}{M}\)
Now we have an expression for the distance \(x_1\) from the pivot to the point through which the object’s weight acts – i.e. the location of the object’s centre of gravity!
Forces experienced by object supports
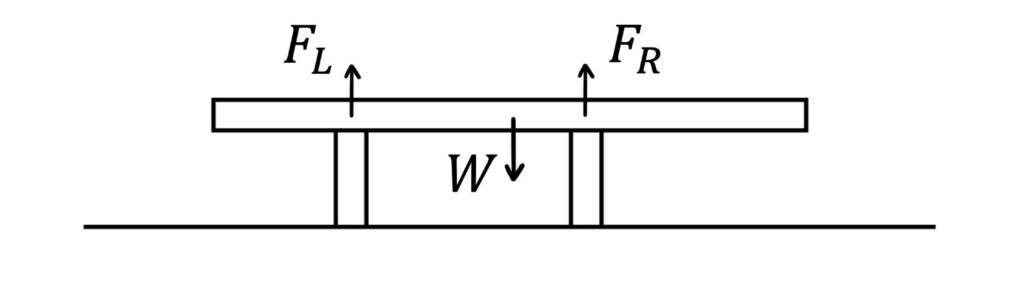
We can use the concept of moments to analyse the forces experienced by object supports.
For example, some objects rest on supports such as chair legs, wheels and scaffold poles. Since the supported object is stationary, its weight \(W\) is balanced by the upward contact forces (\(F_L+F_R\)) exerted by the supports.
If we imagine removing the right support and using our finger instead at the same location, then we need to provide the right support force \(F_R\) while the object is pivoted on the left support:
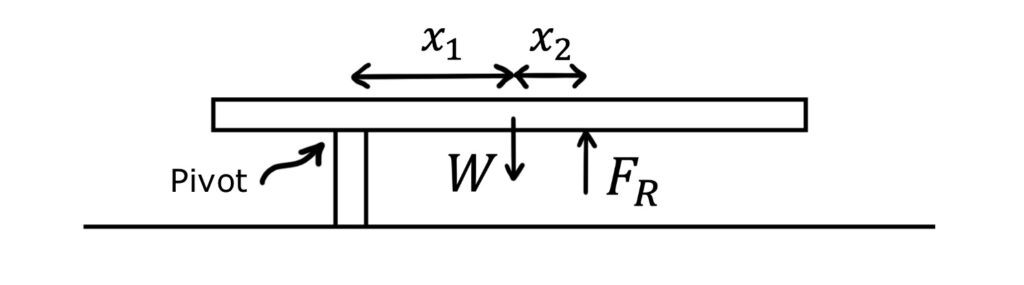
If we hold the object in rotational equilibrium in this position, the clockwise and anticlockwise moments about the pivot balance:
\(Wx_1=F_R(x_1+x_2)\)
Rearranging for \(F_R\) gives:
\(F_R=\frac{Wx_1}{x_1+x_2}\)
Now let’s do the same analysis for the other support. Removing the left support, we support the object using our finger and the object pivots on the right support:
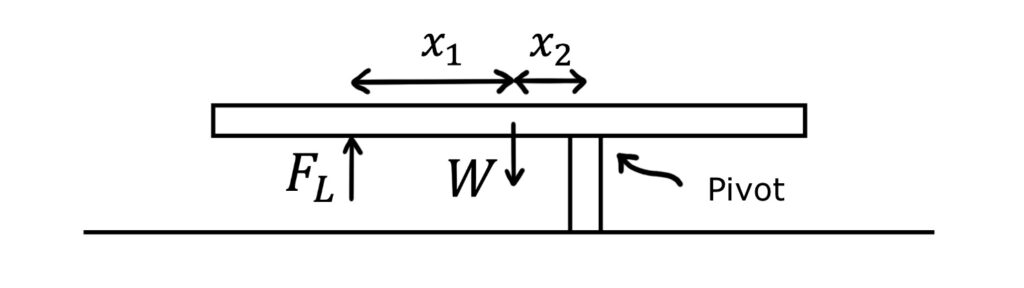
In rotational equilibrium:
\(F_L(x_1+x_2)=Wx_2\)
And rearranging for \(F_L\) we have:
\(F_L=\frac{Wx_2}{x_1+x_2}\)
We now have two expressions for the supporting forces! Notice that they are not equal, and that their relative magnitudes depend on their distances from the centre of gravity of the supported object.
We can now also comment on the forces exerted by the supported object on the supports.
From Newton’s third law, the upward contact force exerted by each support on the object has an equal and opposite downward contact force exerted by the object on the support. Thus, the expressions for \(F_L\) and \(F_R\) are also valid for the counterforces experienced by the supports themselves.
What is a moment of a couple?
Finally, let’s look at something a bit different. Instead of considering systems in rotational equilibrium, let’s look at forces that combine to produce a turning effect.
In particular, let’s consider a couple which is a pair of parallel forces of equal magnitude but opposite directions that cause an object to rotate about an axis.
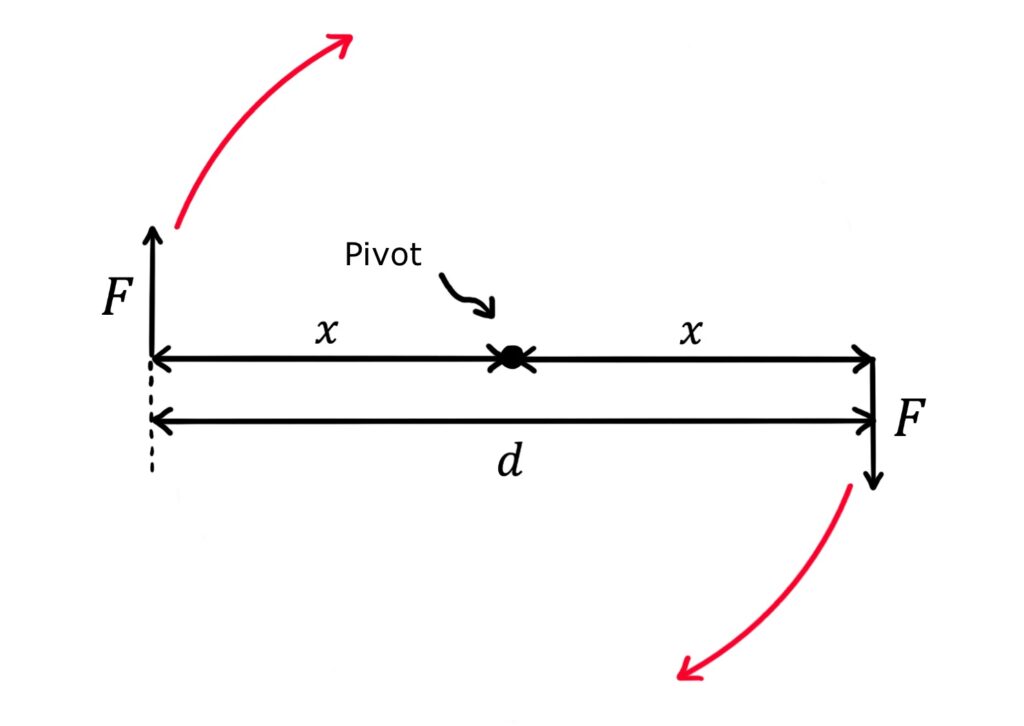
Unlike the situation of rotational equilibrium, the two forces do not create moments in opposite directions, but rather the forces contribute to the same turning effect. The moment of the couple is the sum of the moments of the individual forces:
\(Moment=Fx+Fx\)
\(=2Fx\)
\(=Fd\)
Thus, the moment of the couple is the magnitude of each force \(F\) multiplied by the perpendicular distance \(d\) between the lines of action of the forces.
The moment of a couple is also often called the torque, especially in engineering. Torque is the turning effect of two or more forces.
Conclusion
I hope you’ve enjoyed this review of moments and rotational equilibrium! We’ve learnt about the turning effect of forces, object stability, how to find the centre of gravity of an irregular object, and the unequal forces experienced by object supports.
You might like to consider learning about the related topics of principles of mechanics and circular motion next!
Happy studying!
