Contents
Introduction
In mechanics, an important sub-topic is that of energy, work done, and power.
In this post, we’re going to define the concept of work done, and explore energy transfers, the principle of conservation of energy, power and efficiency.
Let’s begin!
What is work?
Work is the energy transferred to an object by a force acting on the object to make it move. Since work is an amount of energy, it is a scalar quantity measured in joules, \(\rm{J}\).
For example, consider a force \(F\) acting on an object to move it a distance \(s\):
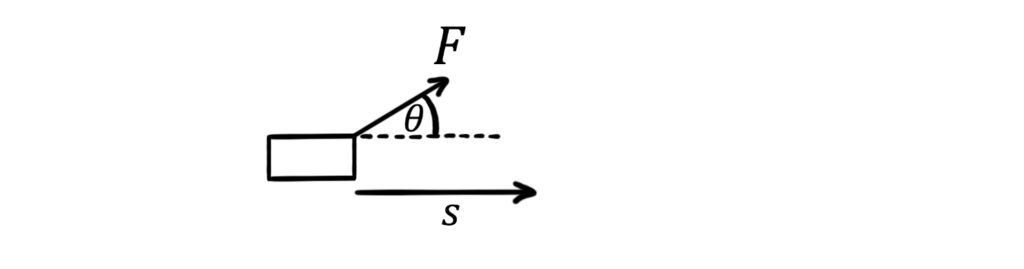
The work done is the force resolved in the direction of the object’s motion multiplied by the distance through which the object moves:
\(W=Fs\cos\theta\)
Of course, when the force is in the same direction as the object’s motion, \(\theta=0^{\circ}\) and \(\cos \theta=1\), so the equation simplifies to this:
\(W=Fs\)
Examples of work done
Let’s apply our equation for work done to a few simple examples.
In a first example, work is done raising a load of mass \(m\) through a height \(h\). The force required to do the work has the same magnitude as the load’s weight because it must be just enough to counteract it. Therefore, \(F=mg\).
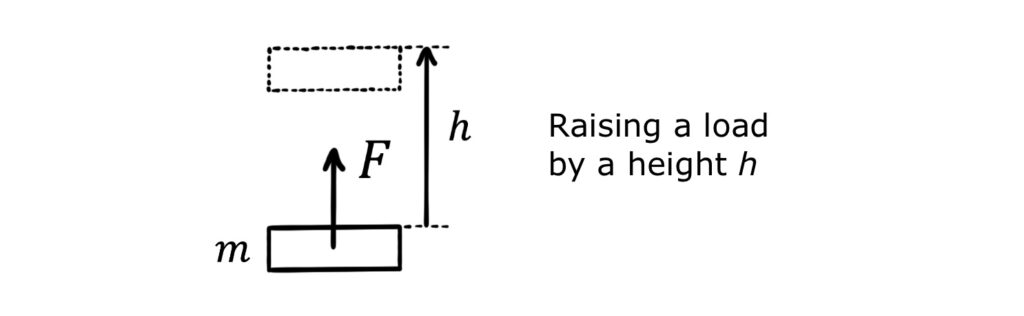
The distance through which the force is applied is \(s=h\), so the work done is:
\(W=Fs=mgh\)
So far so good. Let’s look at a second example, in which work is done stretching a spring by an extension \(x\).
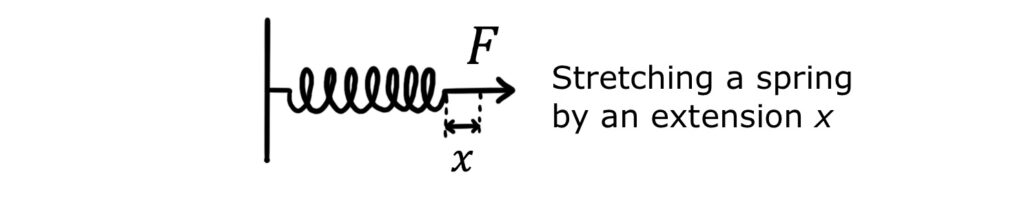
From our knowledge of springs, we know that the force required to extend the spring is not constant, but is proportional to the spring’s extension. So we must use an average force, \(F_{ave}\).
Work done is therefore:
\(W=Fs=F_{ave}x\)
Good stuff! Now let’s try a third and final example. Work is done pulling a trolley a distance \(x\).
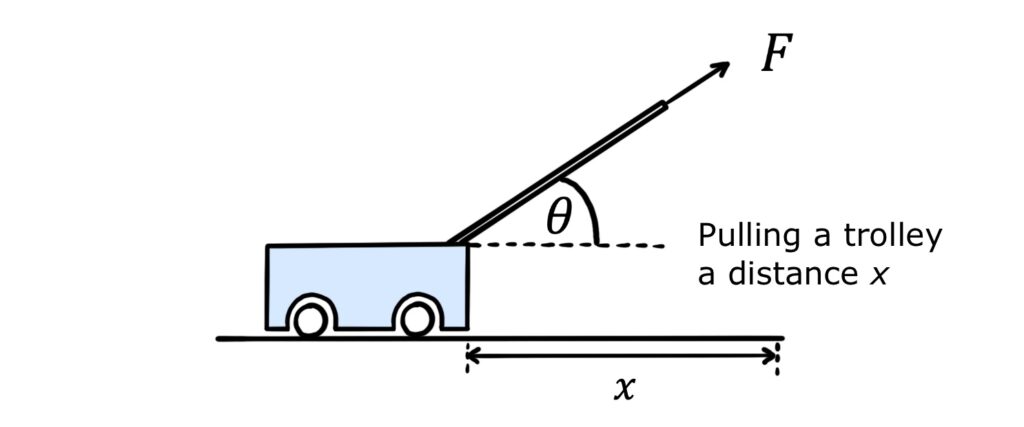
We need to use the component of the force that acts in the direction of motion: i.e. \(F\rm{cos}\,\theta\). Plugging this in with \(s=x\), we have the following expression for work done:
\(W=Fx\cos \theta\)
That was nice and easy!
Area under a force-displacement graph
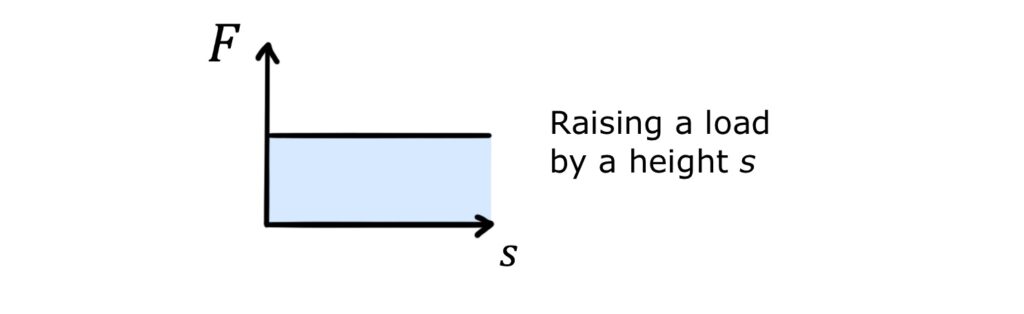
From our definition of work done, the area under a graph of the force (resolved in the direction of the object’s motion) against the distance the object travels is equal to the work done.
In the example of raising a load by a constant upward force, the work done is therefore equal to the area under the constant force line:
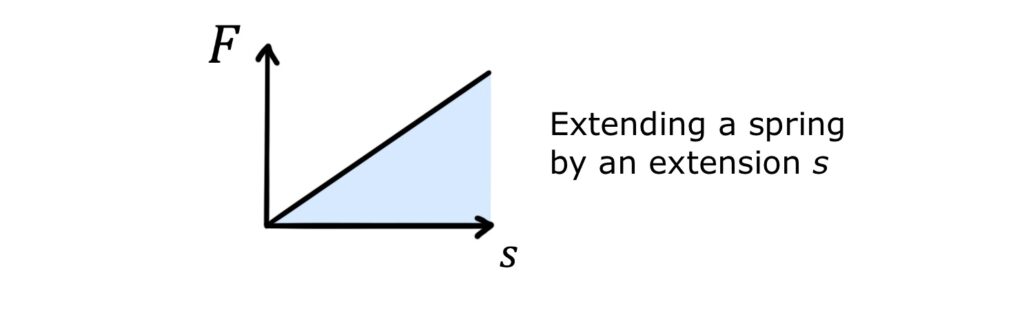
Similarly, in the example of extending a spring, the work done is equal to the area under the line of increasing force:
Transfers between different forms of energy
In all cases, when work is done energy is transferred from one form to another.
For example, if a person does work moving an object, then the energy starts in the form of chemical energy in their muscles. This energy can be transferred to a different form as follows:
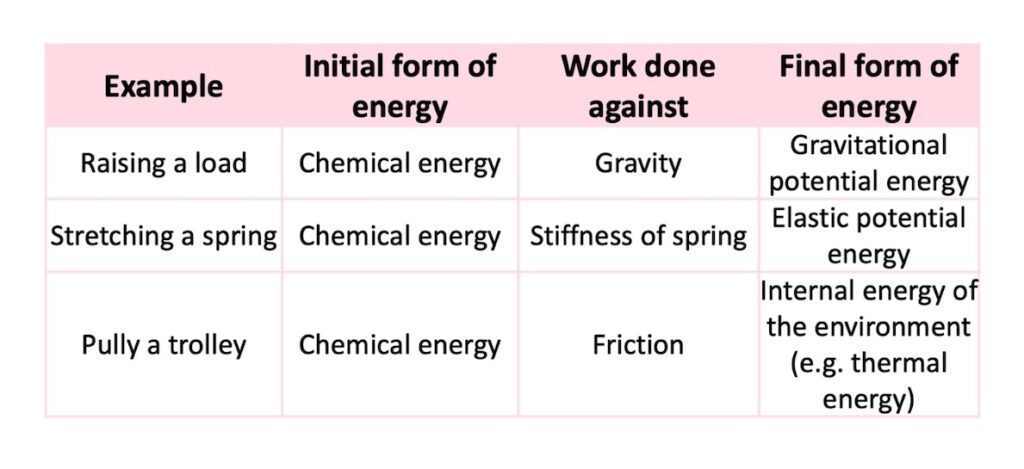
If the work is done by an electric motor, the initial form of the energy is electrical energy.
There are also some common examples of work done that you should be familiar with where energy is exchanged between kinetic energy and gravitational potential energy:
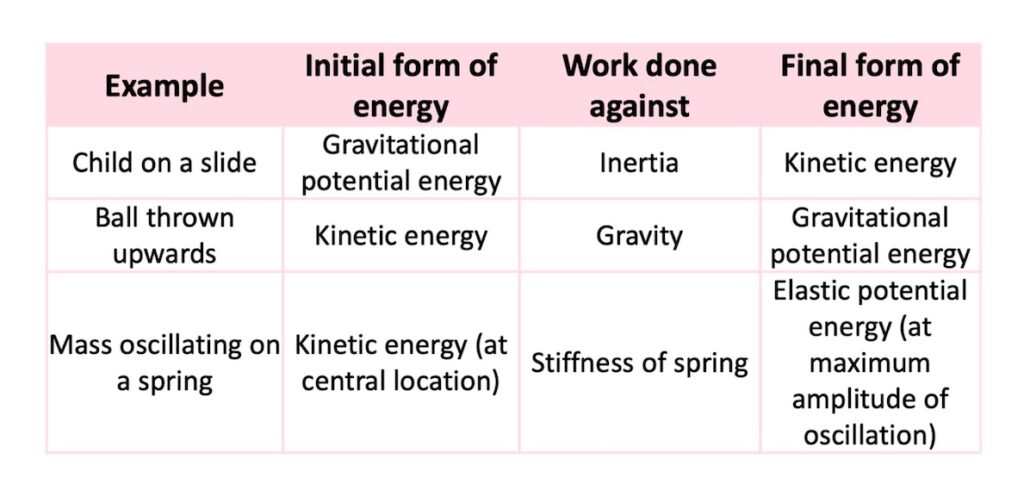
The main thing to remember is that when work is done, energy changes from one form to another!
The principle of conservation of energy
The principle of conservation of energy states that energy cannot be created or destroyed. In a closed system, it can only be transferred from one form to another. This principle is a universal law and applies to all energy transfers in all contexts.
For example, although a pendulum oscillates with a smaller and smaller amplitude over time, this does not mean that energy is disappearing. It is just being transferred to the internal energy of the environment because work is being done against air resistance and friction.
Even in nuclear reactions where energy is converted into mass, no energy is lost because mass is another form of energy (from mass-energy equivalence).
The principle of conservation of energy allows us to do some nifty calculations!
Here’s a classic example. A pendulum is raised to a height \(h\) above its lowest point and let go. We want to find its maximum speed (ignoring air resistance and any friction at the pivot).
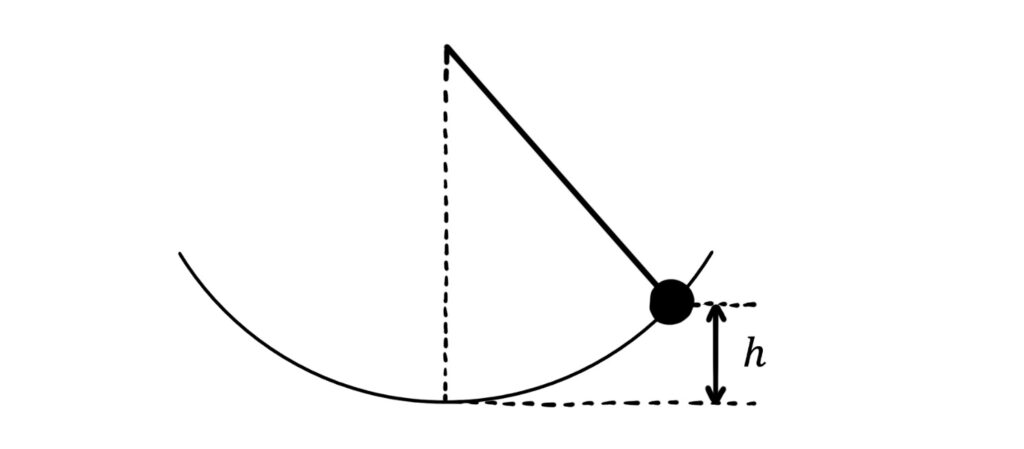
As it swings, its gravitational potential energy is converted to kinetic energy until its lowest point, after which it swings back up and its kinetic energy is converted back into gravitational potential energy.
It therefore has its maximum kinetic energy (and maximum speed, \(v_{max}\)) at its lowest point. At this point, the gravitational potential energy \(mgh\) that it started with has been converted into kinetic energy:
\(\frac{1}{2}mv_{max}^2=mgh\)
Cancelling \(m\) and rearranging, we have:
\(v_{max}^2=2gh\)
So the maximum speed of the pendulum is:
\(v_{max}=\sqrt{2gh}\)
Power
Power is the rate at which energy is transferred from one form to another. So it is equal to the rate of work done:
\(P=\frac{W}{t}\)
It has its own derived unit called the Watt which is equal to one Joule per second: \(1\rm{W}=1Js^{-1}\).
Since \(W=Fs\) (assuming \(F\) is the component of the force in the direction of the object’s motion), we can write:
\(P=\frac{W}{t}=\frac{Fs}{t}\)
However, \(\frac{s}{t}\) is the object’s velocity, so:
\(P=Fv\)
This is another handy expression for power.
Efficiency
Finally, let’s briefly return to the oscillating pendulum. The work it does against air resistance and friction is not useful and can therefore be said to reduce the efficiency of the system.
Efficiency of a system is defined as the useful energy output expressed as a percentage of the energy input:
\(\rm{Efficiency}=\frac{Useful \,energy \,output}{Energy \, input} \times 100\)
Dividing the numerator and denominator by time gives us this alternative expression:
\(\rm{Efficiency}=\frac{Useful \,power \,output}{power \, input} \times 100\)
For example, using the first equation, if a motor transfers \(100\, \rm{J}\) of electrical energy to \(95\, \rm{J}\) of useful kinetic energy and \(5\,\rm{J}\) of energy is dissipated to the environment, then the efficiency of the motor is:
\(\frac{95\,\rm{J}}{100\,\rm{J}} \times 100=95\%\)
Note that efficiency can also be expressed as a fraction if we do not multiply the ratio by \(100\). For example, an efficiency of \(95\%\) could also be expressed as \(0.95\). Either way, efficiency is just a number and has no units.
Conclusion
I hope you’ve enjoyed this review of work, energy and power! This is an important area of mechanics with far-reaching applications.
You might also like to explore the wider principles of mechanics, or other mechanics topics such as projectiles, moments and rotational equilibrium, oscillations, and simple harmonic motion.
Happy studying!
