Contents
Introduction
Stars can be modelled as black body emitters as a result of the characteristic spectrum of electromagnetic radiation they emit.
In this post, we’re going to use the black body emitter model to explore the properties of stellar radiation and see how stars are classified by their spectral output.
Let’s begin!
Stars as black body emitters
A black body emitter is a theoretical object in thermodynamics that absorbs all electromagnetic radiation incident on it. It also emits electromagnetic radiation at all frequencies in a characteristic spectrum.
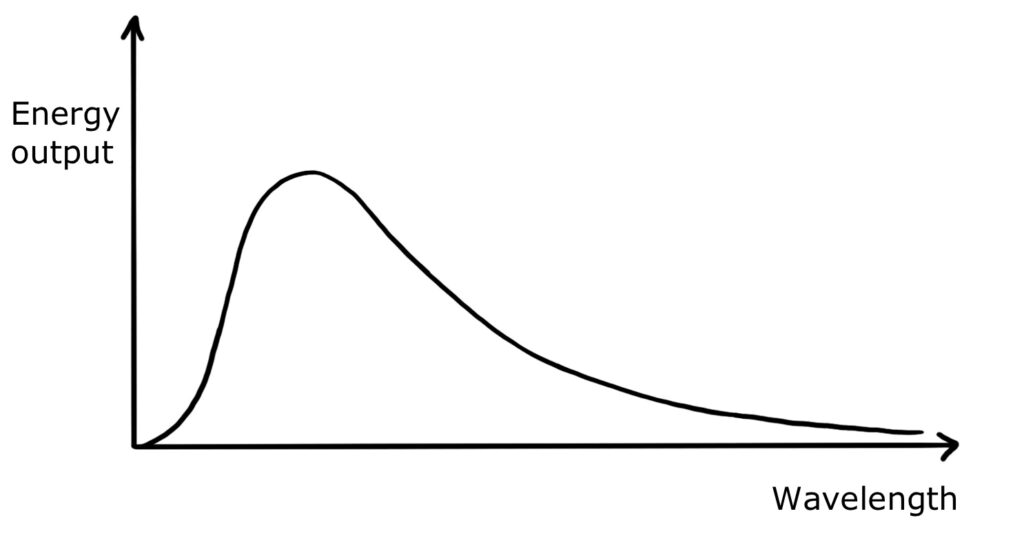
The name ‘black body’ comes from the fact that such objects do not reflect any radiation.
To a good approximation, stars are black body emitters. Wien’s law and the Stefan-Boltzmann law, which are thermodynamic laws for black body emitters, can therefore be used to model the spectral output of stars.
Wien’s law for the peak wavelength of a star
Wien’s law for a black body emitter states that the wavelength at which the body emits the most energy is inversely proportional to the body’s surface temperature:
\(\lambda_{max}T =2.898\times10^{-3}\rm{mK}\)
The wavelength at which the most energy is emitted is called the ‘peak wavelength’ and the constant on the right hand side of the equation is Wien’s constant (in meters-Kelvin).
The peak wavelength of a star can be found by observing the star’s spectral output and finding the wavelength at which the most energy is radiated.
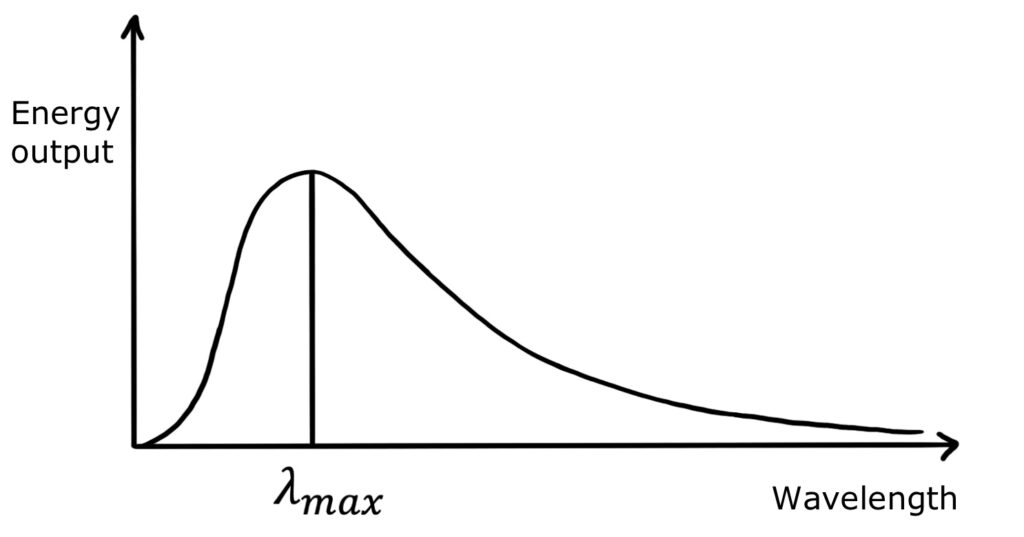
We know from Wien’s law that the surface temperature of a star is inversely proportional to its peak wavelength. Hotter stars therefore have lower peak wavelengths, and their spectra shift to the left:
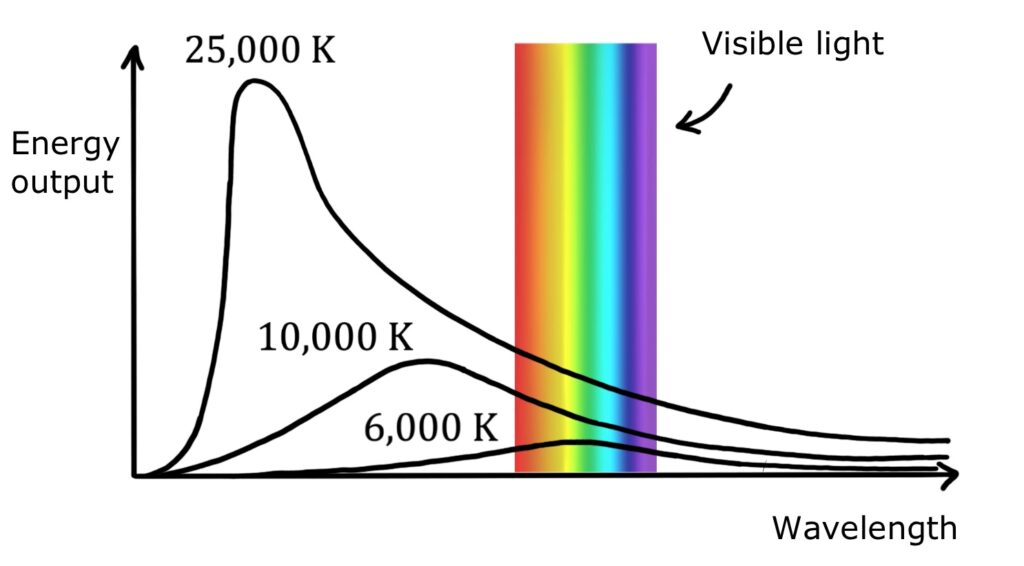
This means that we can observe the spectral output of a star, find its peak wavelength, and use Wien’s law to calculate its surface temperature!
Classification of stars by spectral class
Since peak wavelength depends on surface temperature, stars have been classified into spectral classes based on their surface temperature.
There are seven spectral classes, each corresponding to a surface temperature range.
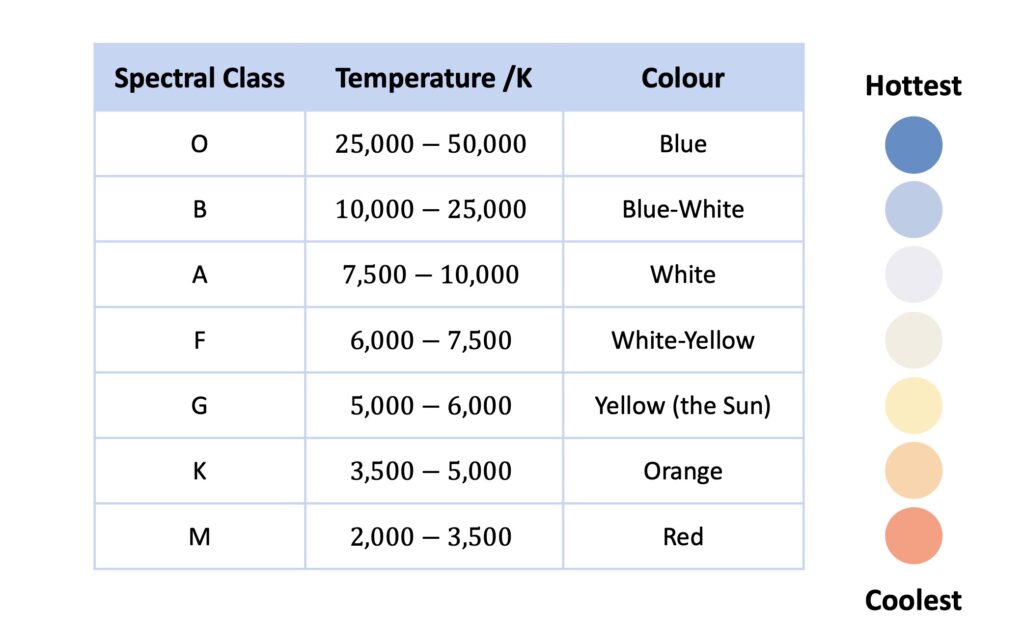
For example, our local star, the Sun, is yellow, has a surface temperature of \(5,775\,\rm{K}\), and belongs to spectral class G. The classes can be easily remembered using the mnemonic Oh Be A Fine Girl/Guy, Kiss Me.
The Stefan-Boltzmann law for total power output of a star
A star’s surface temperature not only determines its peak wavelength, but is also the dominant factor affecting its total power output.
The Stefan-Boltzmann law tells us that the total power output of a star, known as its luminosity, is proportional to its surface area and to the fourth power of its surface temperature:
\(L=\sigma AT^4\)
The constant, sigma, \(\sigma\), is the Stefan-Boltzmann constant.
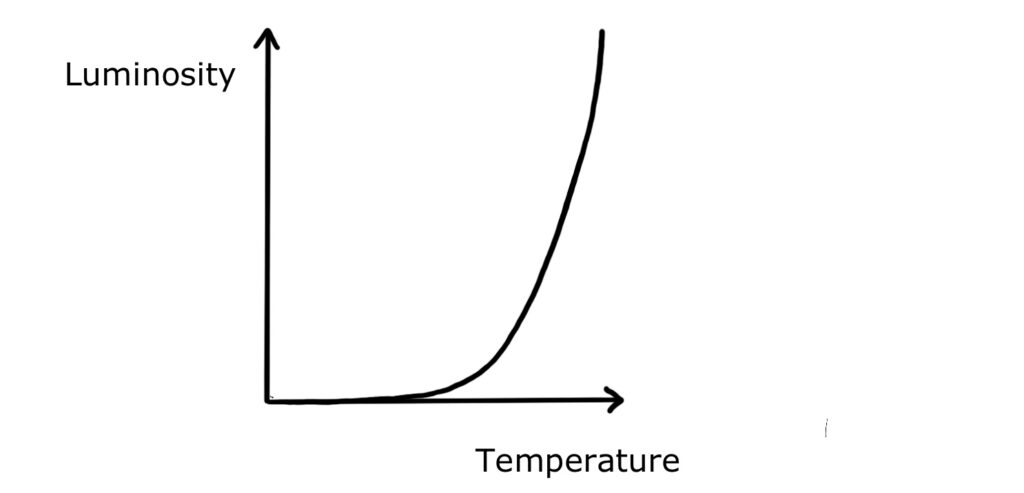
As a result of this relationship, for stars of the same size (and therefore the same surface area, \(A=4\pi r^2\)), luminosity increases rapidly with the fourth power of temperature:
Very massive stars
Very massive stars are stars with a lot of mass.
They have high gravitational pressure at their centre and fast nuclear fusion. This gives them a high surface temperature, and they belong to the hottest spectral classes.
They are also generally large in size, and therefore have a high surface area.
Both of these factors (high surface area and high surface temperature) contribute to a very high luminosity, as we can see from the Stefan-Boltzmann law, \(L=\sigma AT^4\). Their total power output is huge, and can be up to \(800,000\) times more than that of the Sun! 🔆
Conclusion
I hope you have enjoyed this review of stellar radiation! We have seen that stars can be modelled as black body emitters, with their surface temperature dictating their peak wavelength and heavily influencing their luminosity.
Now that you have reviewed this topic, you might like to explore the related and very interesting topics of stellar evolution and nuclear fusion.
Happy studying!
