Contents
Introduction
The SI system of units provides a standardised way of expressing amounts of physical quantities. As such, in order to fully convey your calculated answers in exams it’s essential that you use the correct units for the correct quantities.
In this blog post, we’re going to review base and derived SI units, as well as non-SI units, combination units, and quantities that have no units.
Let’s begin!
What are SI units?
SI units are standard units of measurement agreed by the international scientific community. ‘SI’ stands for ‘Système International’ which is French for ‘international system’.
The SI system has seven base units which may be combined to form other units. Combinations of SI base units that have their own name and symbol are called SI derived units.
Let’s take a closer look at SI base units and SI derived units.
SI base units
There are seven SI base units as follows:
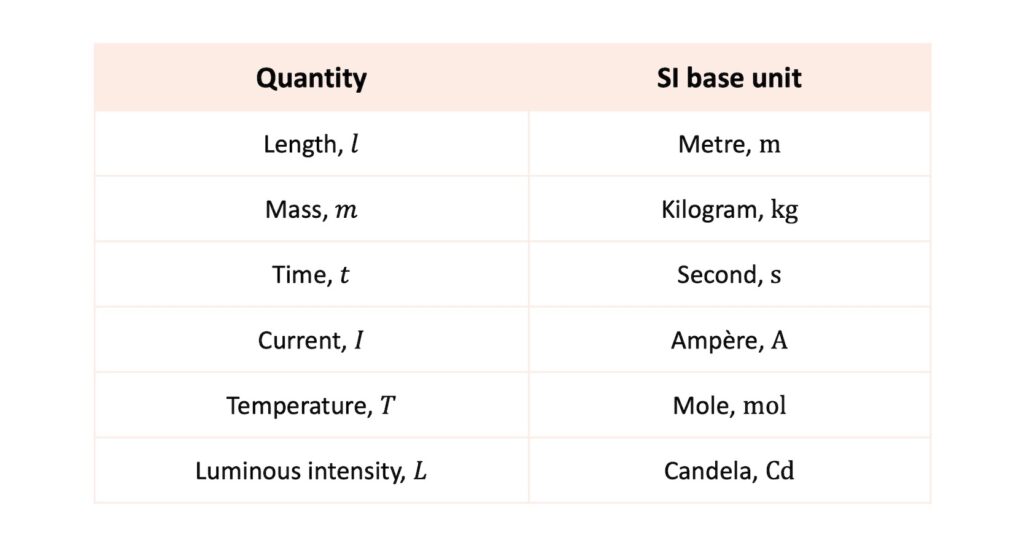
These seven base units form a set from which all other SI units can be derived. Thus, they form the foundation of the SI system of units and are defined by reference to physical phenomena.
For example, the SI unit of time, the second, is defined as \(9,192,631,770\) periods \((T=\frac{1}{f})\) of a photon having energy equal to the difference between two specific energy levels of a caesium-133 atom.
Similarly, the SI unit of length, the metre, is defined as the distance travelled by light in a vacuum during \(\frac{1}{299,792,458}\) of a second (where the second is defined as above).
You don’t need to know these definitions, you only need to be aware that the base units are defined with respect to physical phenomena and that they form the foundation of the SI system of units.
SI derived units
SI derived units are combinations of base units and they have their own names and symbols.
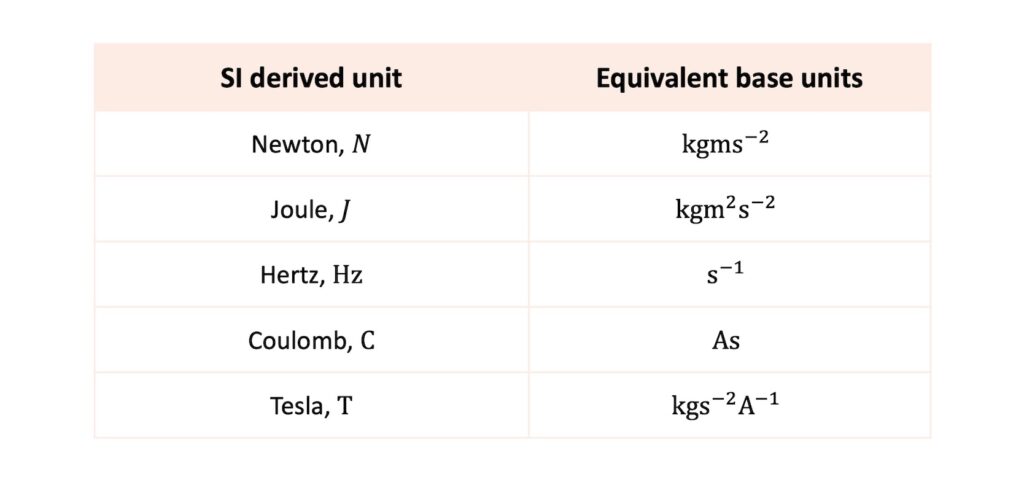
For example, force is measured in Newtons, \(\mathrm{N}\). The Newton is a derived unit and is equivalent to the kilogram-metre-per-second-squared: \(\mathrm{kgms^{-2}}\).
How do we know the equivalent base units of a derived unit?
The answer is that we can work them out using the equation for the quantity having the derived unit.
For example, force is given by the equation \(F=ma\). The units on each side of the equation must balance, so one Newton is equal to the unit of mass multiplied by the unit of acceleration: \(\mathrm{kg\times ms^{-2}}\). Thus, \(\mathrm{N} = \mathrm{kgms^{-2}}\).
It is therefore super-easy to work out the equivalent base units of an SI derived unit!
Here are a few more examples of SI derived units and their equivalent base units:
Non-SI units
So far, we have looked at SI base units and SI derived units. But some quantities also have non-SI units that are particularly suited to specific contexts.
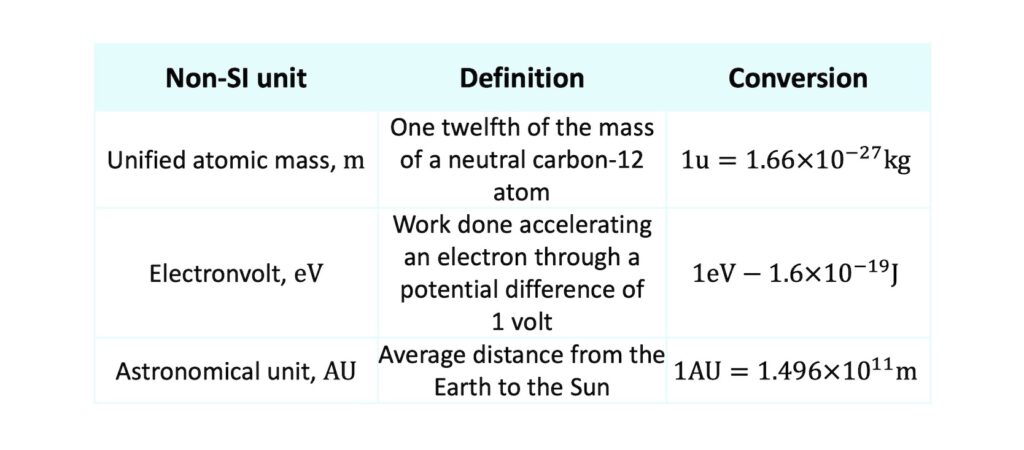
For example, in nuclear physics particles have tiny masses and it would be inconvenient to deal with kilograms which are ridiculously large compared to tiny nucleons. Therefore, the unified atomic mass, \(\mathrm{u}\), which is defined as one twelfth of the mass of a neutral carbon-12 atom, is routinely used. This small mass unit is equivalent to \(1.66\times10^{-27}\mathrm{kg}\).
Other examples of specialised non-SI units arise in atomic physics for expressing small amounts of energy and in astrophysics for expressing large distances:
Quantities with no units
Let’s not forget that some quantities have no units at all! Typically, these arise when the definition of the quantity involves a ratio of two quantities having the same dimensions (e.g. a ratio of lengths or a ratio of masses).
For example, the following quantities have no units and you can see that their definitions involve ratios of quantities with the same dimension:

Quantities with combination units
Last but not least, there are many quantities whose units do not have a special name of their own but which are a combination of other units. Many of these are made from base units, but some also involve derived units or even non-SI units!
Just like derived units, these combined units can generally be worked out from the equation defining the quantity.
For example, density is defined as mass per volume: \(p=\frac{m}{V}\). Balancing units on each side of the equation tells us that the unit for density is equal to the unit for mass divided by the unit for volume. This gives us a combined unit for density of \(\mathrm{kgm^{-3}}\).
Even the unit \(\mathrm{m^3}\) for volume is a combined unit based on the equation for volume being length cubed: \(V=l^3\).
In another example, intensity is power per area: \(I=\frac{P}{A}\). The unit for intensity can therefore be expressed as the unit for power (Watts) divided by the unit for area (\(\mathrm{m^2}\)): \(\mathrm{Wm^{-2}}\). Note that this combined unit is not made up exclusively of base units. The Watt is a derived unit, while the metre is a base unit.
I don’t recommend you necessarily learn all the combined units you come across. Familiarity with common ones is valuable, but you can generally work out combined units from the quantity’s equation (which you should definitely learn).
Prefixes
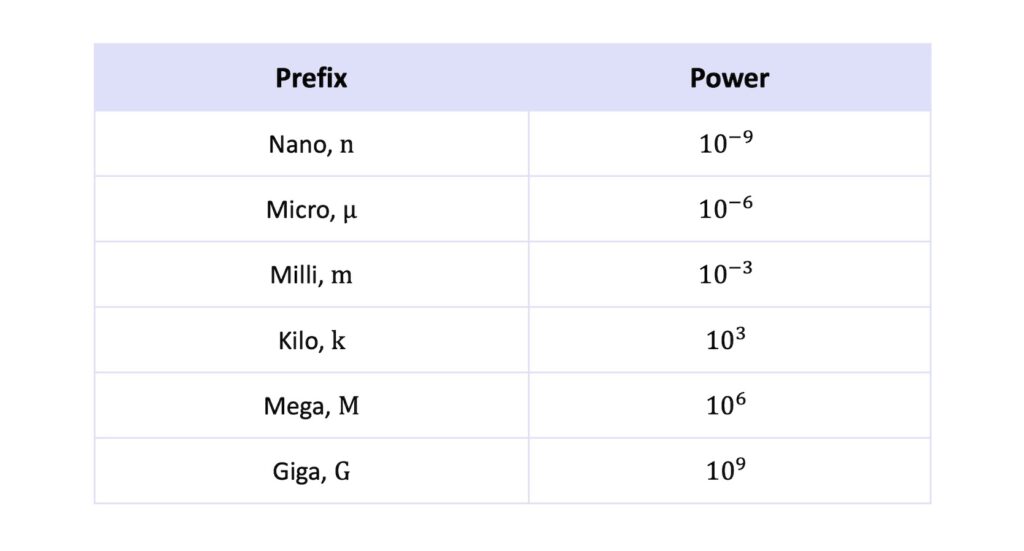
Finally, you should know at least the common prefixes used to express standard form notation from \(10^{-9}\) to \(10^{9}\).
Here they are!
Summary
To help you take away the key points about the system of units, I have summarised them for you in this infographic:

Conclusion
I hope you’ve enjoyed this review of the SI system of units!
From the SI base units and derived units to non-SI units and quantities with no units, it’s worth familiarising yourself with the units system. I recommend learning the base units as well as some of the key derived, combined and non-SI units. This will help you feel confident about presenting your calculated answers in exams and even score you some easy marks!
Happy studying!
