Contents
Introduction
Capacitors are important little devices that store electrical energy by holding accumulated charge on their metallic plates. For a given potential difference placed across them, they are designed to hold as much charge as possible.
But what happens when groups of capacitors are combined in an electrical circuit?
In this post, we’re going to explore the composite behaviour of groups of capacitors, including their total capacitance and the total amount of charge they can store.
Let’s begin!
Equation for capacitance
Capacitance is defined as the amount of charge a capacitor can store on each of its plates per volt of potential difference placed across it:
\(C=\frac{Q}{V}\)
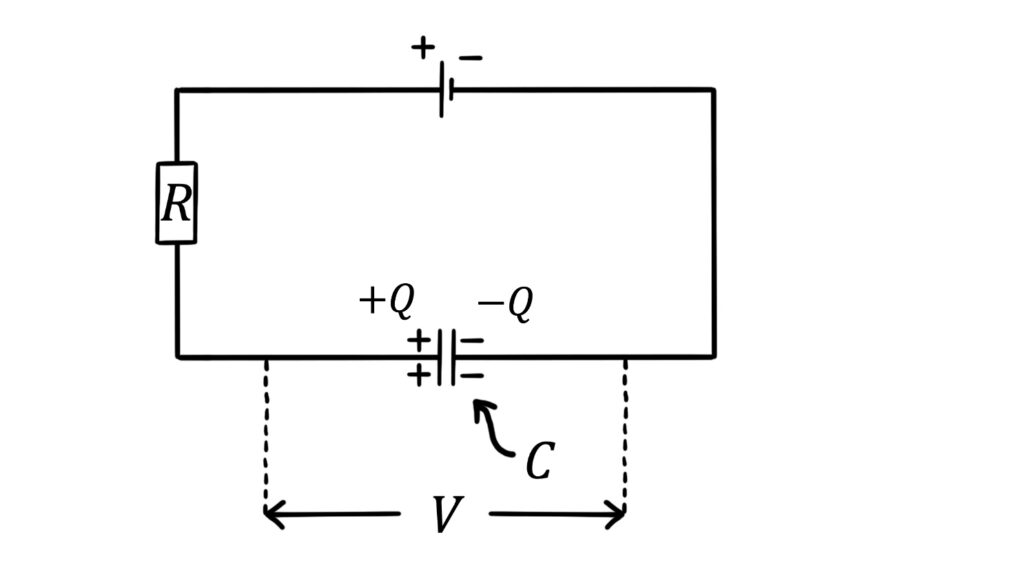
Calculating capacitance is therefore simple in the case of a single capacitor.
However, when multiple capacitors are combined together, we need to adapt this equation to find the total capacitance of the group.
Let’s see how this plays out for (1) capacitors in parallel and (2) capacitors in series.
Capacitors in parallel
When capacitors are placed in parallel in a circuit, the potential difference, \(V\), across each capacitor is the same:
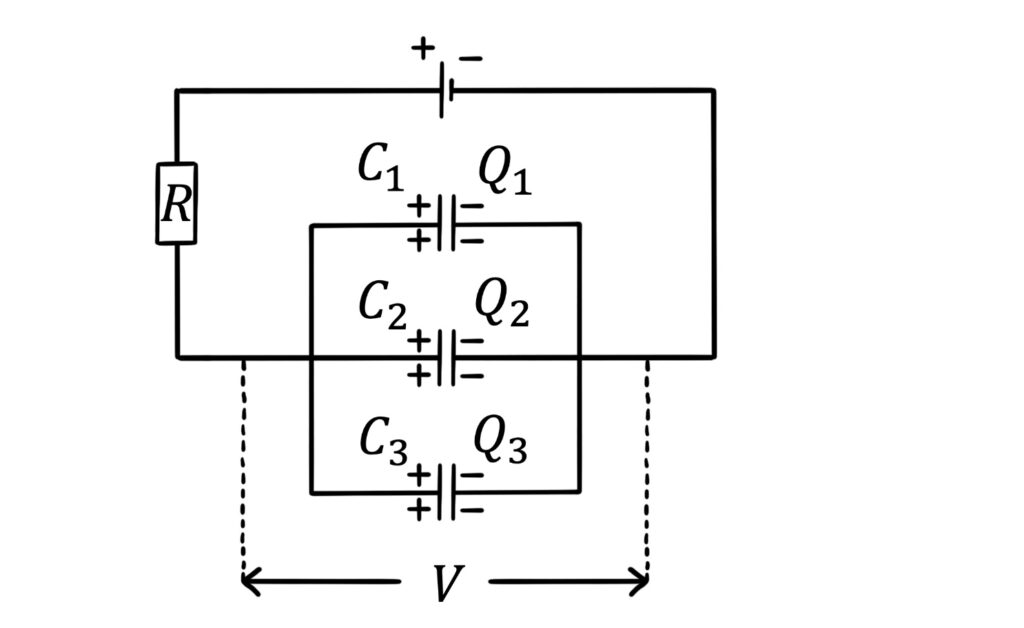
We can also see that the total charge stored by the parallel arrangement is the sum of the individual charges: \(Q=Q_1+Q_2+Q_3\).
These facts enable us to calculate the total capacitance of the group.
From the definition of capacitance above, we can say that the total capacitance is:
\(C=\frac{Q}{V}\)
Since the total charge is \(Q=Q_1+Q_2+Q_3\) and the potential difference across the whole group is \(V\), we have:
\(C=\frac{Q_1+Q_2+Q_3}{V}\)
But for each capacitor, \(Q_1=C_1V\) etc, so we can rewrite this as:
\(C=\frac{C_1V+C_2V+C_3V}{V}\)
The potential difference cancels and this simplifies to:
\(C=C_1+C_2+C_3\)
Thus, the total capacitance is the sum of the individual capacitances!
In summary, for capacitors in parallel:
- Potential difference across each capacitor is the same
- Since \(Q_1=C_1V\) etc for each capacitor, the charge each capacitor stores depends on its capacitance
- Total charge stored is \(Q=Q_1+Q_2+Q_3\)
- Total capacitance is \(C=C_1+C_2+C_3\)
Capacitors in series
By contrast, when capacitors are placed in series, the potential difference across each capacitor is different:
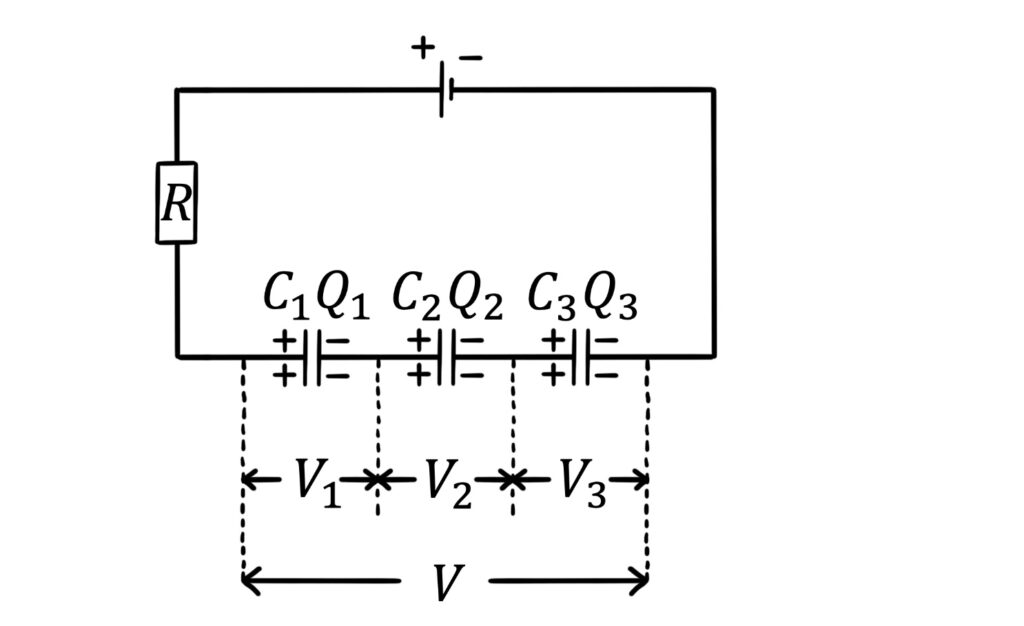
We can also appreciate that the only capacitor plates that are actually connected to the circuit in this arrangement are the outermost plates (i.e. the left plate of capacitor 1 and the right plate of capacitor 3). This is because the other plates are electrically isolated from rest of the circuit by the insulating dielectric layers in the middle of each capacitor.
As a result, during charging the cell only directly charges the two outermost plates. The other plates acquire charges of equal magnitude by virtue of the attraction or repulsion of their electrons to or from the charged outer-most plates. (For example, electrons flow from the left plate of capacitor 2 to the right plate of capacitor 1.) All the capacitors therefore store the same amount of charge: \(Q_1=Q_2=Q_3\)
Since the only plates connected to the circuit are the outermost plates, the composite arrangement behaves like a capacitor whose two plates are the outermost plates and which stores the charges on those plates.
Consequently, the total charge stored by the group is equal to the charge stored on the outer-most plates: \(Q=Q_1=Q_2=Q_3\)
Using these facts, we can now calculate the total capacitance of the group.
From the definition of capacitance above, we can say that the total capacitance is:
\(C=\frac{Q}{V}\)
Since the potential difference across the group is \(V=V_1+V_2+V_3\) and the charge stored by the group is \(Q\), we have:
\(C=\frac{Q}{V_1+V_2+V_3}\)
Inverting both sides gives:
\(\frac{1}{C}=\frac{V_1+V_2+V_3}{Q}\)
For each capacitor, \(Q=C_1V_1\) etc, so we can rewrite this as:
\(\frac{1}{C}=\frac{Q/C_1+Q/C_2+Q/C_3}{Q}\)
The charge cancels and this simplifies to:
\(\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\)
Thus, the inverse of the total capacitance is the sum of the inverses of the individual capacitances!
In summary, for capacitors in series:
- Potential difference across each capacitor is different
- Total charge stored is \(Q=Q_1=Q_2=Q_3\)
- Since \(Q=C_1V_1\) etc for each capacitor, the pd across each capacitor depends on its capacitance
- Total capacitance is given by \(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\)
Other combinations
More complex arrangements are of course possible. These could, for example, include a parallel arrangement of series groupings, or a series arrangement of parallel groupings.
In such cases, the total capacitance of the sub-groups can be calculated first, and then these sub-groups can be combined to find the total capacitance of the arrangement as a whole.
Conclusion
I hope you’ve enjoyed learning about combinations of capacitors! If you haven’t done so already, you might like to take a look at the structure of capacitors to find out how they are specially designed to store as much electrical energy as possible.
Happy studying!
