Contents
Introduction
The Standard Model of particle physics describes the elementary particles, the ways they can combine, and how they interact with each other through the four fundamental forces.
In this post, we’re going to look at composite particles, their main features, and their roles in everyday matter.
Let’s begin!
Composite particles are made from quarks
Composite particles can be formed by combinations of quarks which are elementary particles of the Standard Model:
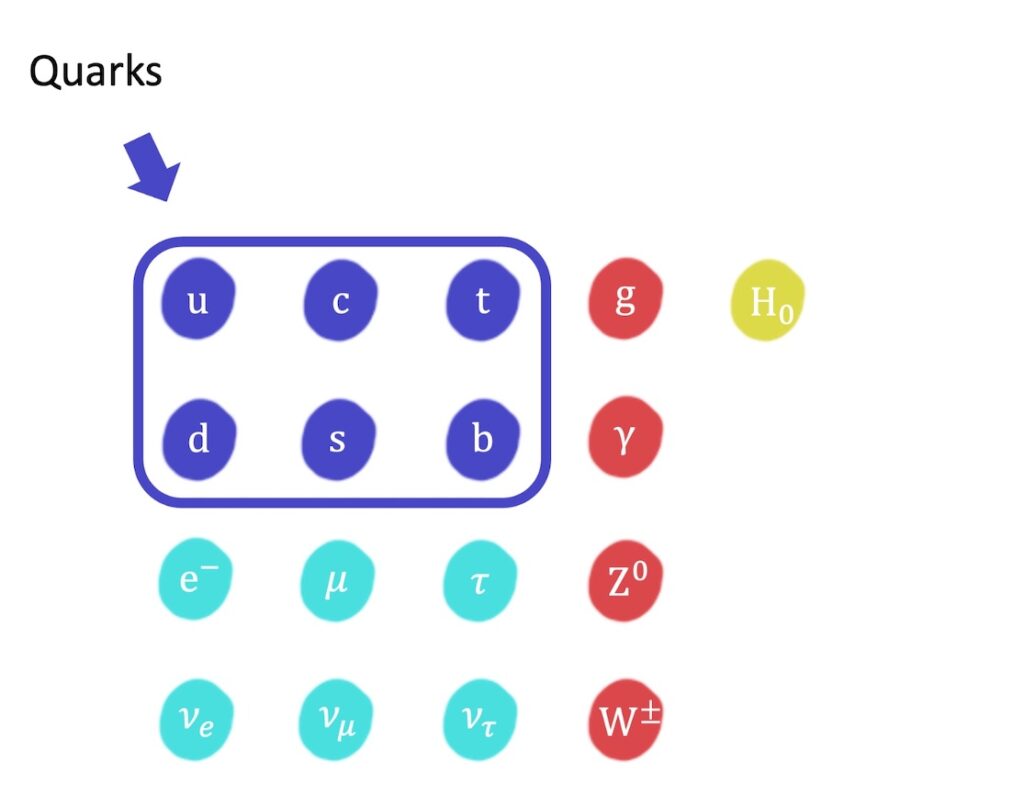
Quarks are the only elementary particles to feel the strong nuclear force and it is this force that holds them together to form composite particles.
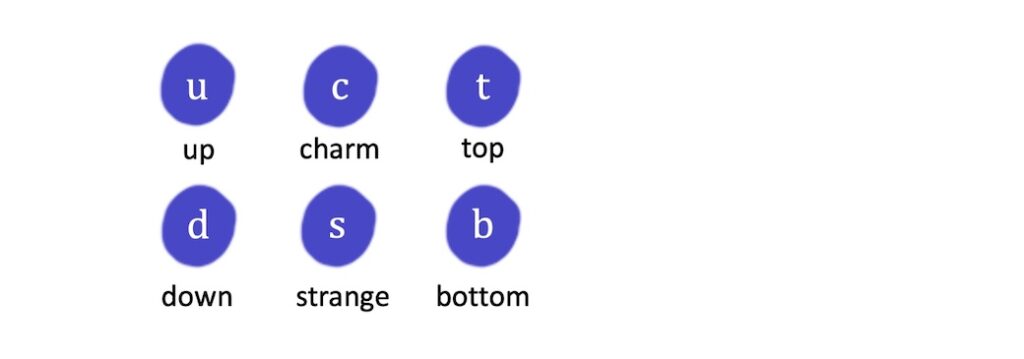
There are six members of the quark family, dividing into three pairs: the up and down quarks, the charm and strange quarks, and the top and bottom quarks:
All of these can combine in various ways to form composites. Quark composites are called hadrons, and they divide into two families: baryons and mesons. Here are some examples of each:

As you can see, the familiar proton and neutron of the atomic nucleus belong to the baryon family! These baryons therefore play an important role in everyday matter.
We’re going to be looking at the properties of some of these baryons and mesons, so it will be handy to know the properties of their constituent quarks. All quarks have a spin of \(1 \big/ 2\), and the up, charm and top quarks have a charge of \(2 \big/ 3\), while the down, strange and bottom quarks have a charge of \(-1 \big/ 3\).
What are baryons?
Baryons are quark composites made from three quarks.
For example:
- The proton has a quark composition of \(\mathrm{uud}\)
- The neutron has a quark composition of \(\mathrm{udd}\)
- The Xi-minus has a quark composition of \(\mathrm{dss}\)
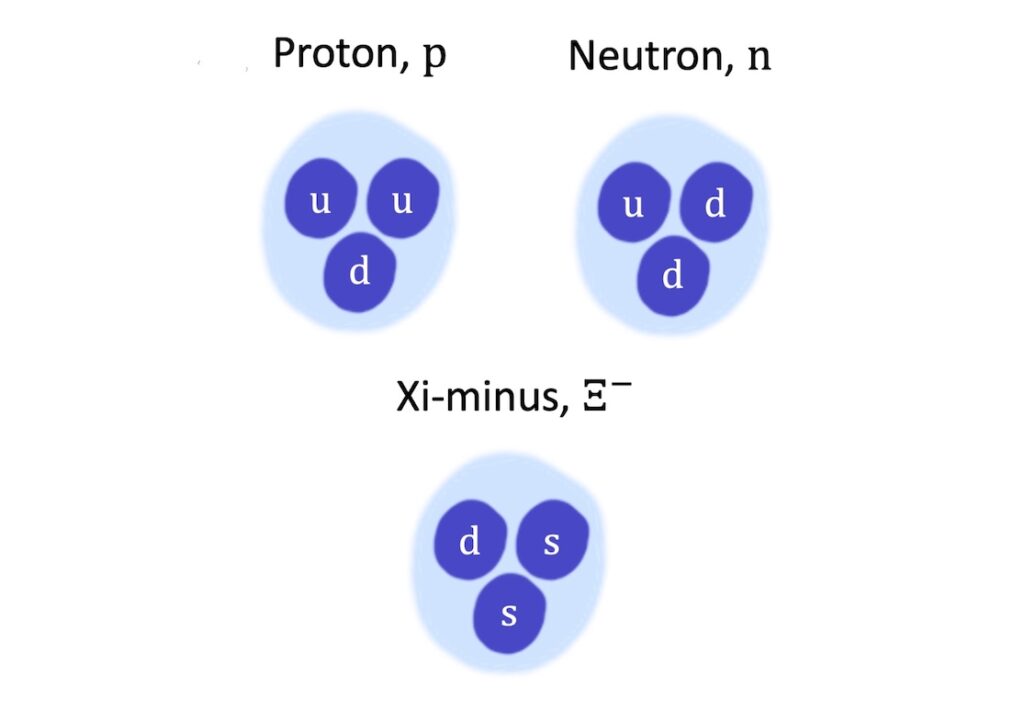
As you might expect, the overall properties of these composite particles depend on the properties of their constituent quarks.
For example, the overall charge of a baryon is just the sum of the charges of its constituent quarks. The charge of a proton (\(\mathrm{uud}\)) is therefore \(2 \big/ 3 + 2 \big/ 3 – 1 \big/ 3=1\).
Similarly, the overall strangeness of a baryon is the sum of the strangenesses of its constituent quarks. (The strange quark has a strangeness of \(-1\) and the other quarks have a strangeness of \(0\).) The strangeness of the Xi-minus particle (\(\mathrm{dss}\)), for example, is therefore \(0-1-1=-2\).
Spin is a bit different. Although each quark has a spin of \(1 \big/ 2\), the spins either add or subtract depending on whether they are aligned.
In a baryon, all three spins can be aligned or one spin can be misaligned with the others:
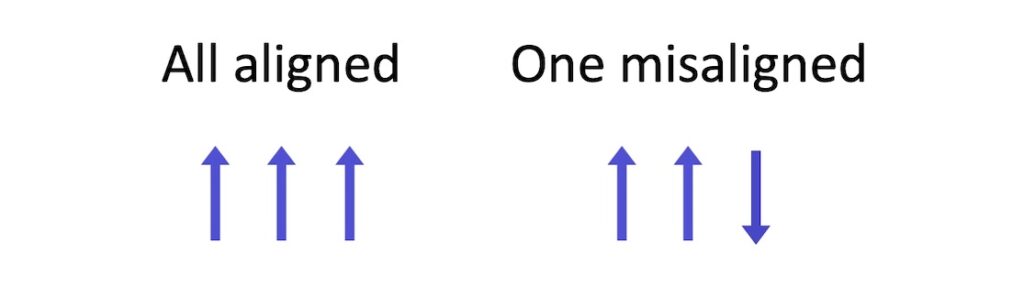
If they are all aligned, the overall spin is \(1 \big/ 2 + 1 \big/ 2 + 1 \big/ 2=3 \big/ 2\). If one is misaligned, the overall spin is \(1 \big/ 2 + 1 \big/ 2 – 1 \big/ 2=1 \big/ 2\).
For each of the above example baryons, the overall spin is \(1 \big/ 2\), revealing that in these baryons one quark’s spin is misaligned with the others.
Baryons also have another property that is specially defined for them. This is baryon number, and all baryons have a baryon number of \(1\). Quarks each have a baryon number of \(1 \big/ 3\), and all other particles have a baryon number of \(0\).
The various properties of the above example baryons are summarised as follows:
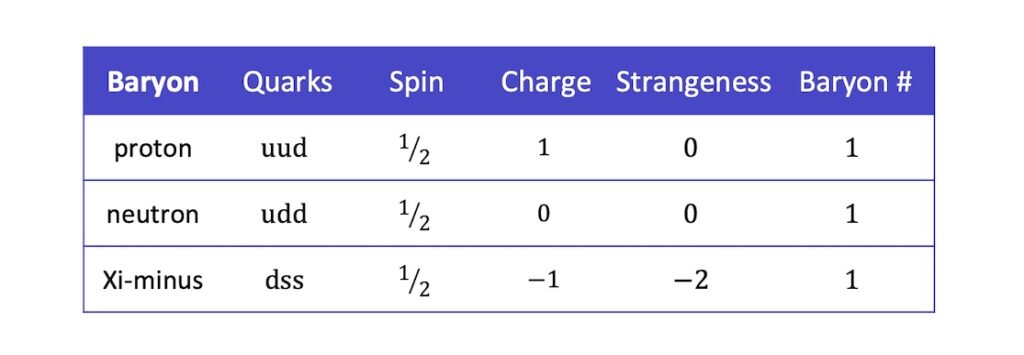
It’s interesting to note that the constituent quarks of the proton and the neutron are the up and down quarks. These are the lightest of the six quarks and therefore the most stable.
Just like elementary particles, baryons also have corresponding antiparticles. In antibaryons, the constituent quarks are just swapped for the corresponding antiquarks. For example, the proton has a quark composition of \(\mathrm{uud}\), and the antiproton has \(\mathrm{\overline{u}\overline{u}\overline{d}}\).
What are mesons?
Mesons are more exotic hadrons made from a quark and an antiquark.

For example:
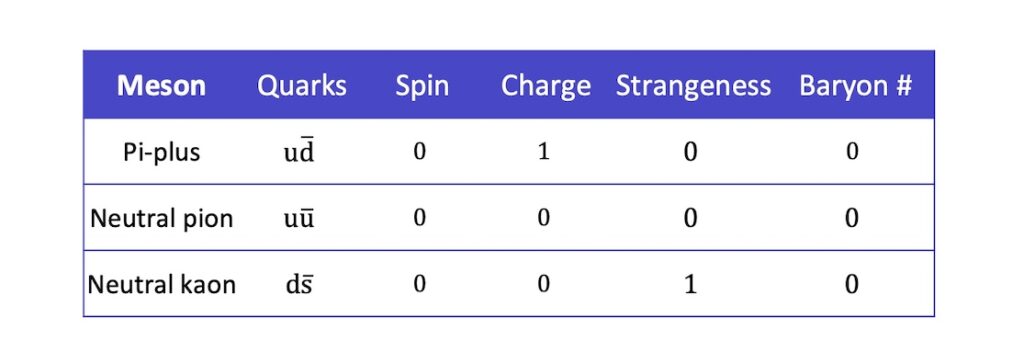
- The Pi-plus has a quark composition of \(\mathrm{u\overline{d}}\)
- The neutral pion has a quark composition of \(\mathrm{u\overline{u}}\)
- The neutral kaon has a quark composition of \(\mathrm{d\overline{s}}\)
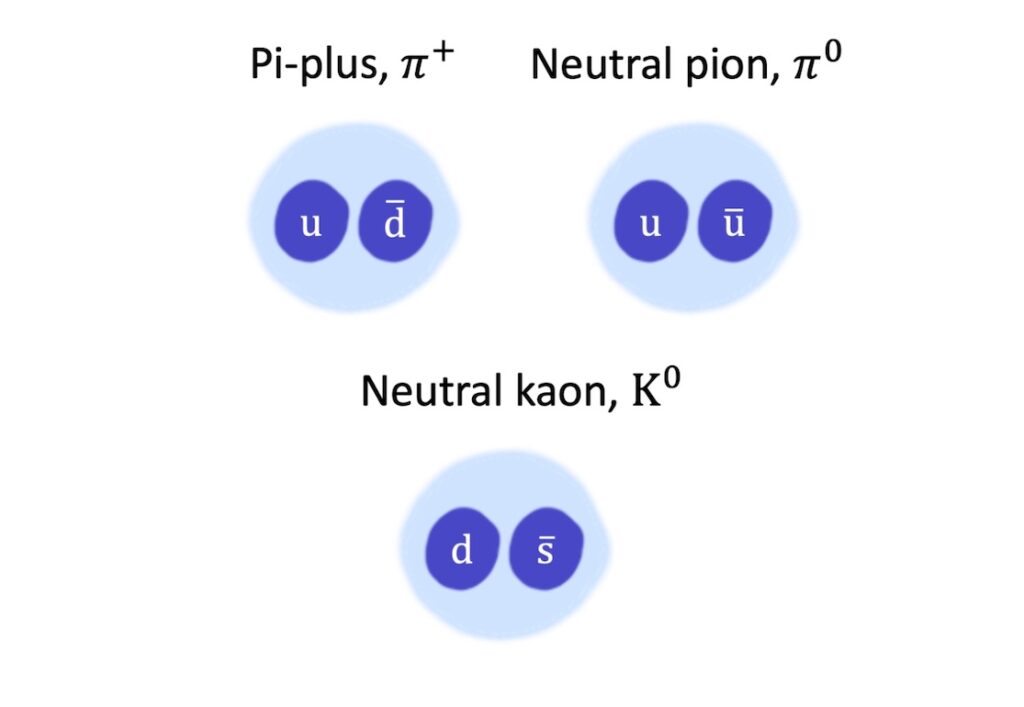
To find the properties of these composite particles, the same rules apply. The charge, strangeness and baryon number of the constituent quark and anti-quark add up, and the spins add or subtract depending on whether they are aligned.
In a meson, the two spins can either be aligned or misaligned:

If they are aligned, the meson has a spin of \(1 \big/ 2 + 1 \big/ 2=1\), and if they are misaligned the meson has a spin of \(1 \big/ 2 – 1 \big/ 2=0\).
These properties of the above example mesons are summarised as follows:
Just like baryons, mesons have antiparticles where the constituent quark is swapped for its antiquark and the constituent antiquark is swapped for its quark. For example, the pi-plus particle has a quark constitution of \(\mathrm{u\overline{d}}\) and its antiparticle has a quark constitution of \(\mathrm{\overline{u}d}\).
You may have noticed that some mesons are made from a quark and that same quark’s antiparticle. In that case, the meson is its own antiparticle. For example, the neutral pion, \(\mathrm{u\overline{u}}\), is its own antiparticle.
Mesons are highly unstable composites. They only exist in very high energy environments and decay quickly into more stable particles.
The significance of spin
As we have seen, baryons can have spins of \(1 \big/ 2\) or \(3 \big/ 2\) and mesons can have spins of \(0\) or \(1\).
This is very significant because particles with half integral spin are fermions (particles of matter) and particles with integral spin are bosons (non-matter particles).

This is a profound difference between baryons and mesons because fermions and bosons behave very differently.
Conclusion
I hope you’ve enjoyed this review of the composite particles! It’s super interesting to see how quarks can combine to form such diverse composites.
Next you might like to explore the system of classification of particles in the Standard Model, the full range of elementary particles, or the related topics of particle reactions and nuclear physics.
Happy studying!
