Contents
Introduction
Electrostatic forces are very strong, belonging to the second strongest of the four fundamental forces, the unified electromagnetic force. Electric fields also have an infinite range and can be produced by both positive and negative charges.
In this post, we’re going to review the key properties of electric fields and look at the electrostatic interactions they create.
Let’s begin!
Coulomb’s law of electrostatics
Coulomb’s law gives us an equation for the electrostatic force \(F\) between two charges \(Q\) and \(q\) separated by a displacement of \(r\):
\(F=\frac{kQq}{r^2}\)
Coulomb’s constant, \(k\), is given by \(k=\frac{1}{4\pi {\epsilon}_0}\).
This important equation is an inverse square law, with \(F\) decreasing with \(\frac{1}{r^2}\). In the case of like charges (i.e. \(Q\) and \(q\) either both positive or both negative), \(F\) is positive and a graph of force against displacement looks like this:
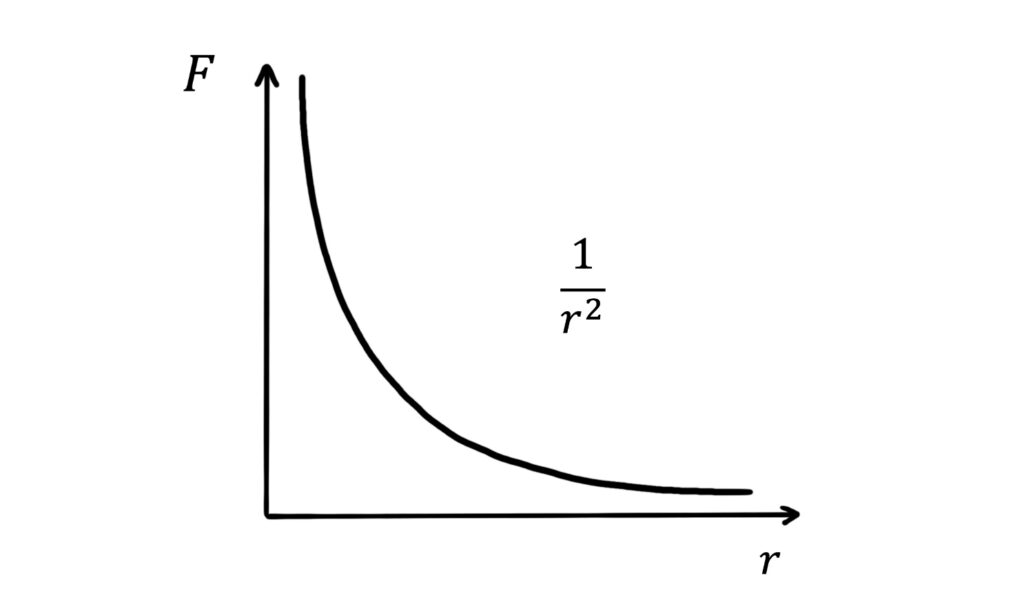
For unlike charges, \(F\) takes negative values like this:
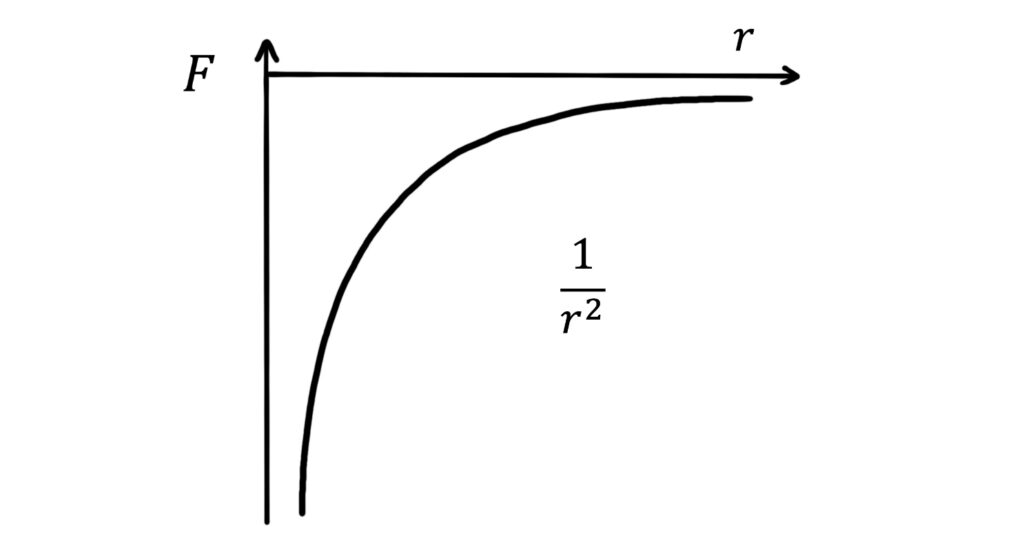
In either case, we can see that the force reaches a value of zero only when \(r=\infty\). Electric fields therefore have an infinite range.
It is conventional to treat \(Q\) as the source of the field (at the centre of the field), with \(q\) being located somewhere in the field at a displacement of \(r\) from \(Q\). We can then define the positive direction with \(r\):
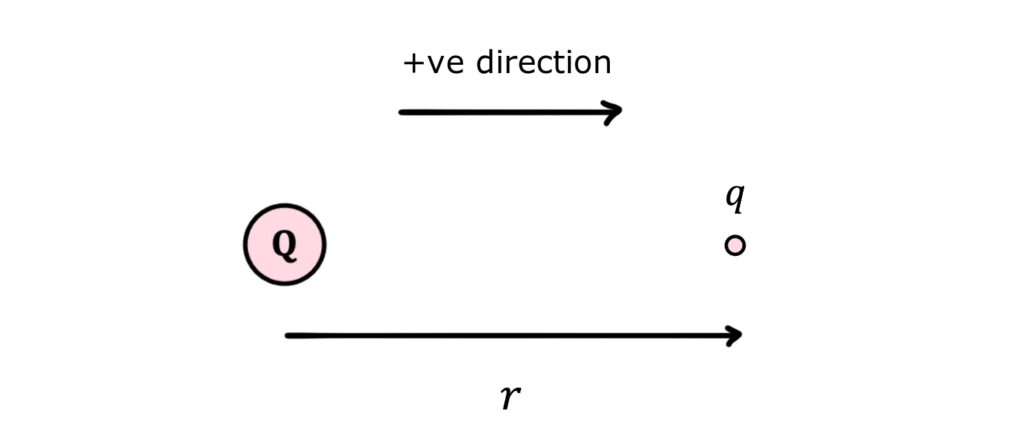
For example, for two positive charges, \(F\) is positive and points in the positive direction away from the source of the field:

By contrast, for a positive \(Q\) and a negative \(q\), \(F\) is negative and points in the negative direction towards the source of the field:

Radial electric fields
Coulomb’s law tells us that the force experienced by charge \(q\) in \(Q\)’s field varies only with \(r\) (since \(k\), \(Q\) and \(q\) are constants). The electric field around \(Q\) is therefore radial because it extends into space in the same way in all directions.
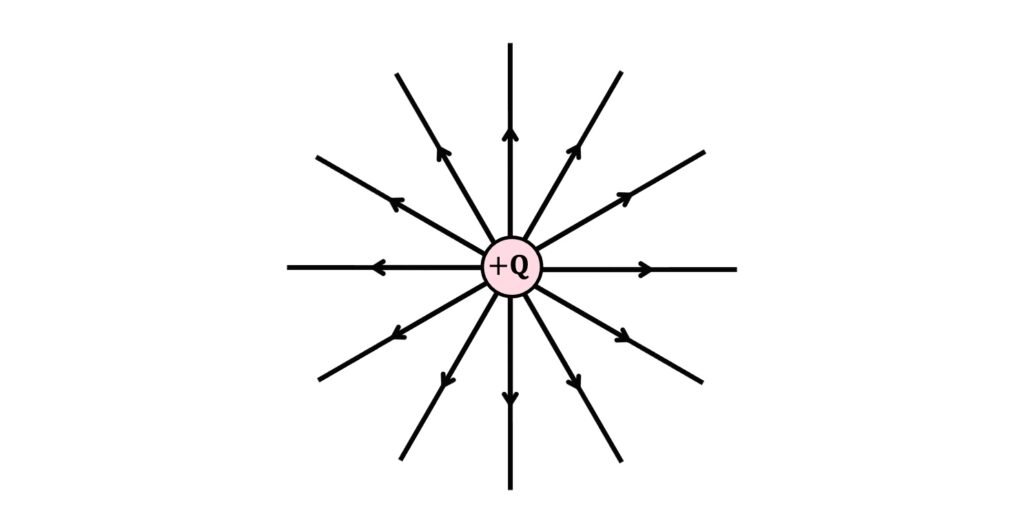
We can express this radial shape of an electric field using field lines. These represent the direction of the force a positive charge \(+q\) would experience at each point in the field.
For example, a field with a positive source, \(+Q\), repels \(+q\) away from the centre of the field, so the field lines point outwards:
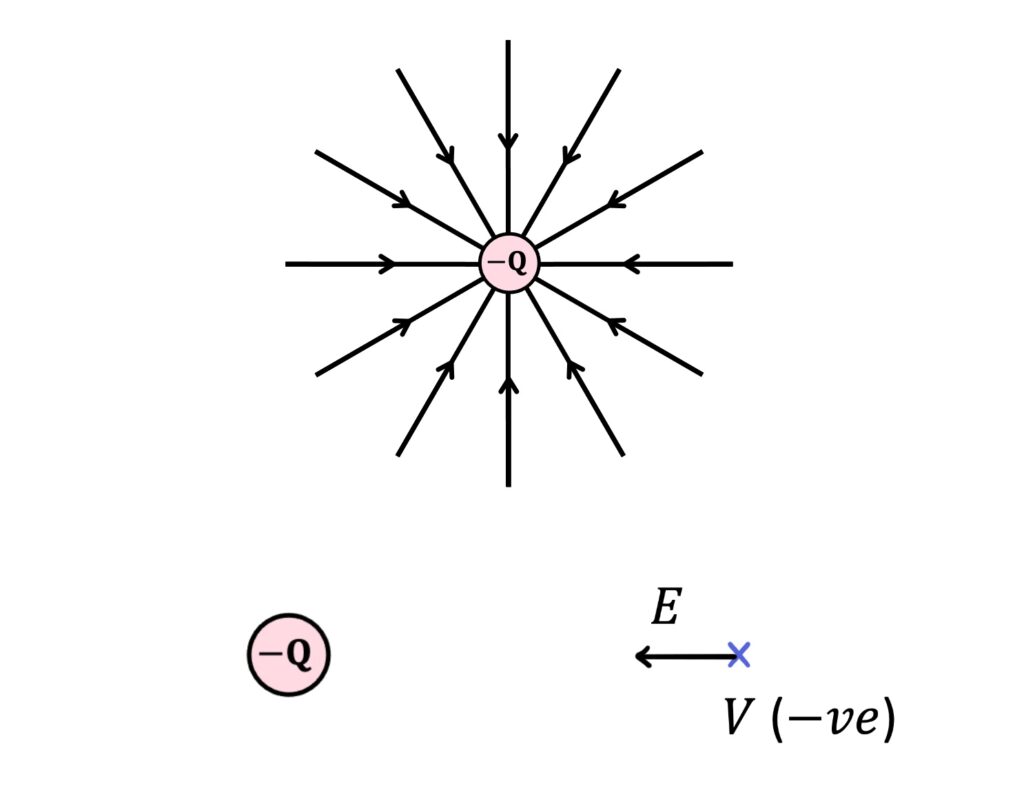
On the other hand, a field with a negative source, \(-Q\), attracts \(+q\) towards the centre of the field, so the field lines point inwards:
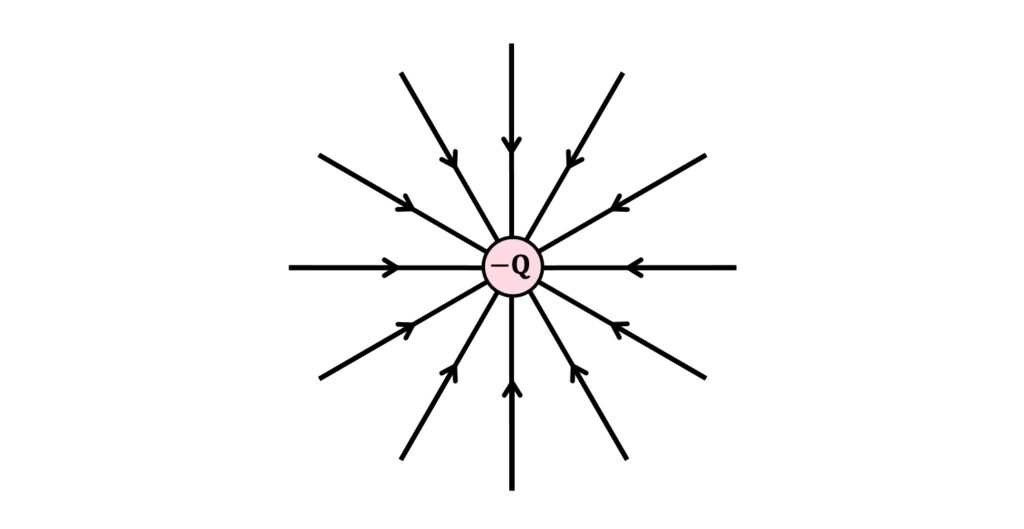
How to calculate electric field strength
Electric field strength \(E\) at a point in an electric field is the force unit positive charge would experience at that point in the field. For a positive source, \(+Q\), field strength \(E\) therefore points outwards:

Since field strength is equal to force per unit charge, we can calculate it by dividing the above expression for force by \(q\). Field strength is therefore given by:
\(E=\frac{kQ}{r^2}\)
This is another inverse square law, with \(E\) decreasing with \(\frac{1}{r^2}\):
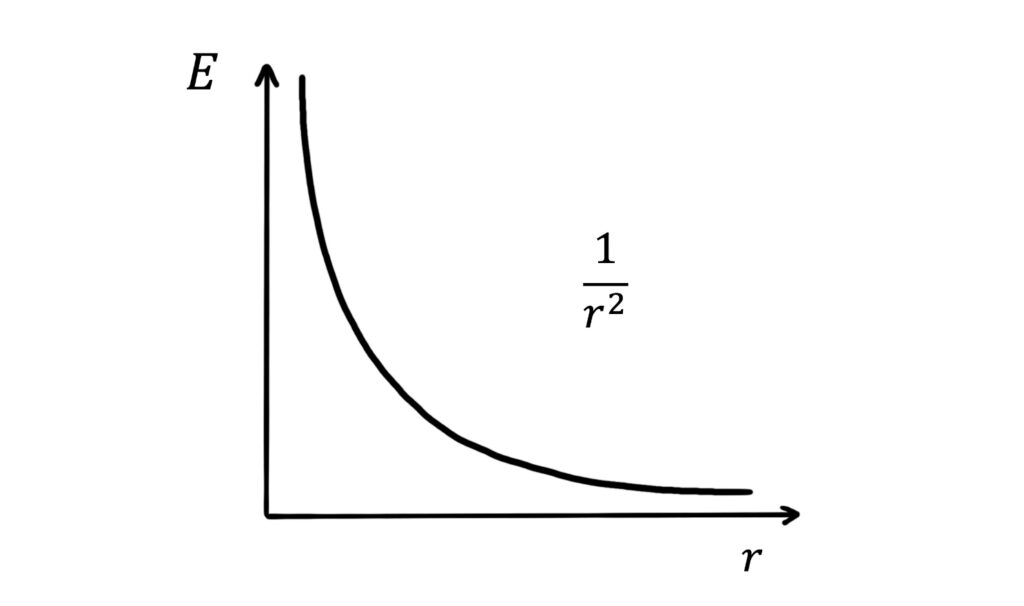
We can also see from this expression that electric field strength reaches zero only when \(r=\infty\), consistent with the infinite range of electric fields.
How to calculate electric potential energy
Electric potential energy \(E_{pot}\) is the energy stored by a charge \(q\) by virtue of being held at a point in an electric field.
For positive \(Q\) and \(q\), \(E_{pot}\) is positive:

To understand why, imagine that a charge \(+q\) is so far away from the centre of the field that it is located at \(r=\infty\). It is effectively outside the field. As such, it can’t be affected by the field and its electric potential energy is zero.
If we move this charge to a position of \(r<\infty\), it moves into the field and gains some electric potential energy. But since both charges are positive, they repel each other and we have to do work to push the charge into the field. We have therefore supplied energy, and so the charge’s electrical potential energy increases. Since it started at zero, it is now positive.
(Conversely, a charge \(-q\) will fall from \(r=\infty\) into the field of \(+Q\), and therefore its resulting electric potential energy will be negative.)
An expression for electric potential energy can be derived by considering the work done moving a charge from \(r=\infty\) to \(r<\infty\) into an electric field. The full derivation involves calculus and is outside the scope of A Level physics, but it is based on the familiar equation
\(work \,done=force \times\,distance\)
with \(F=\frac{kQq}{r^2}\) from Coulomb’s law.
This results in the following expression for electric potential energy!
\(E_{pot}=\frac{kQq}{r}\)
This is an inverse relationship between \(E_{pot}\) and \(r\), with \(E_{pot}\) taking positive values for like charges:
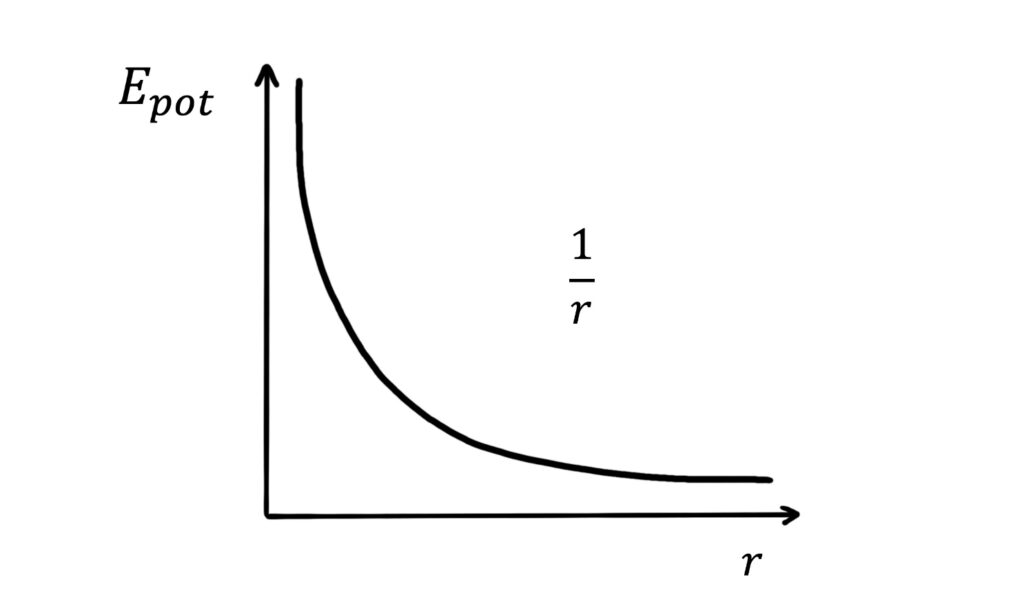
What is electric potential?
Like electric field strength, electric potential \(V\) is a property of the field itself. Electric potential is the electric potential energy unit positive charge would have at a given point in the electric field:

It is therefore equal to the electric potential energy \(E_{pot}\) of an object divided by its charge \(q\):
\(V=\frac{kQ}{r}\)
This is another \(\frac{1}{r}\) relationship in which \(V\) takes positive values for positive \(Q\):
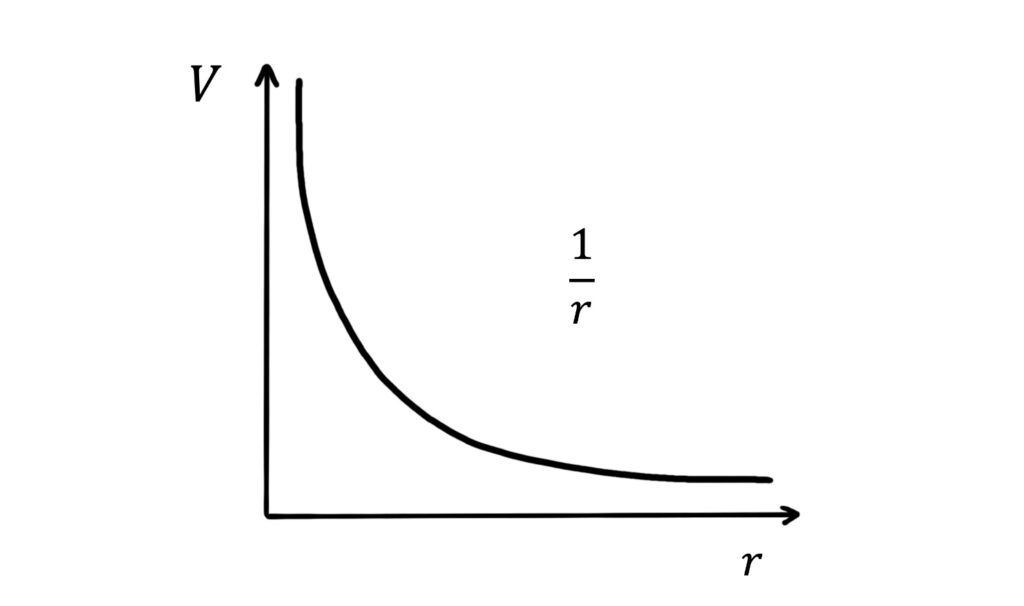
Electrostatic equipotential lines
In addition to the field lines we saw above, another useful way of visualising an electric field is to use equipotential lines which represent regions of equal electric potential. In a radial field, these are regions of fixed \(r\), which are circles (or, in three dimensions, spheres):
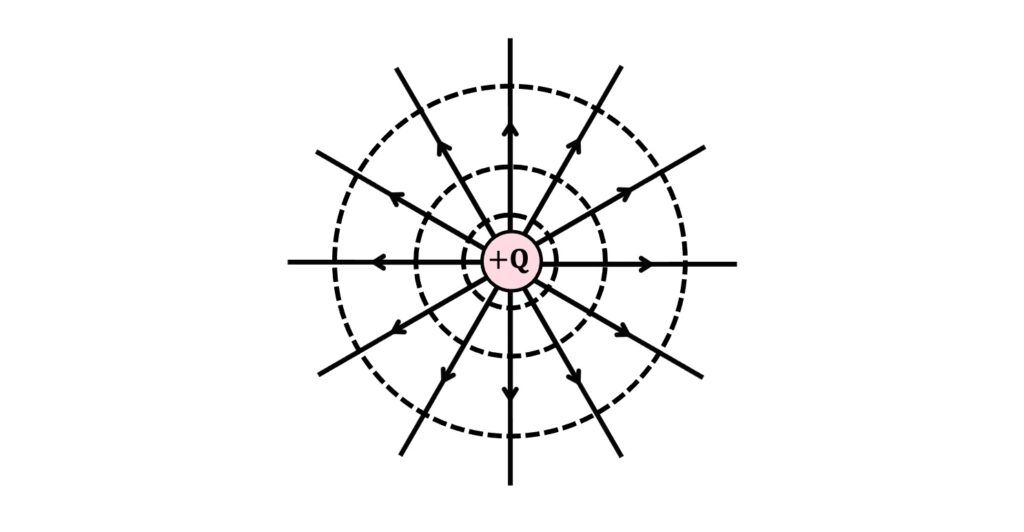
The difference in electric potential between adjacent equipotentials is fixed, but as we go further away from the centre of the field the equipotentials become further apart. The reason for this can be seen clearly from the \(V\)-\(r\) graph:
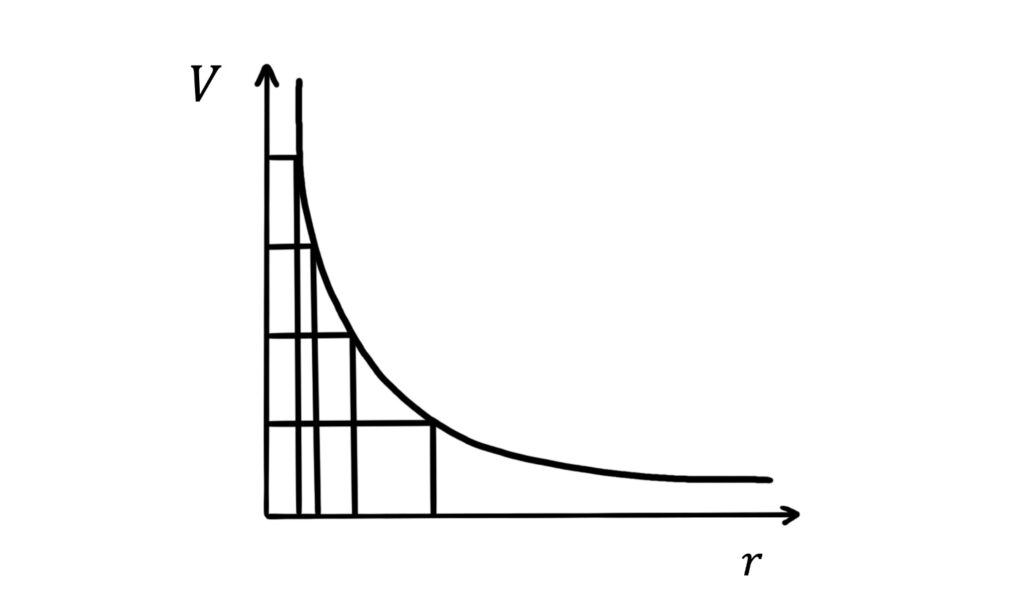
The relationship between electric potential and electric field strength
Electric potential and electric field strength are both properties of the electric field and they have an interesting relationship with each other.
The gradient of a \(V\)-\(r\) graph is equal to the magnitude of the field strength.
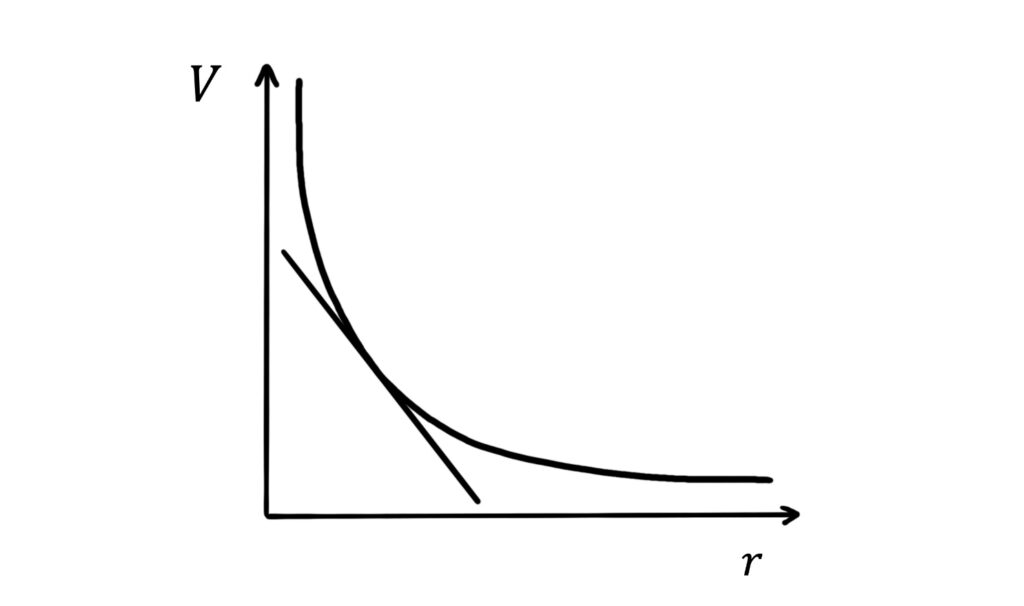
For a positive source, \(+Q\), the field strength is positive. However, the gradient of the \(V\)-\(r\) graph is negative, so electric field strength is equal to minus this gradient:
\(E=-\frac{\Delta V}{\Delta r}\)
This makes intuitive sense. In a region of greater field strength (higher \(E\)), it takes more work (\(\Delta V\)) to push unit positive charge a displacement of \(-\Delta r\) (towards the centre of the field).
Work done moving a charge in an electric field
It’s easy to find an expression for the work done moving a charge \(q\) a displacement \(\Delta r\) away from the centre of an electric field.

We know that the work done is equal to the change in the object’s electric potential energy:
\(\Delta E_{pot}=\frac{kQq}{\Delta r}\)
Since we can also write \(\Delta V=\frac{kQ}{\Delta r}\) from the definition of electric potential, we can express work done as:
\(\Delta W=q\Delta V\)
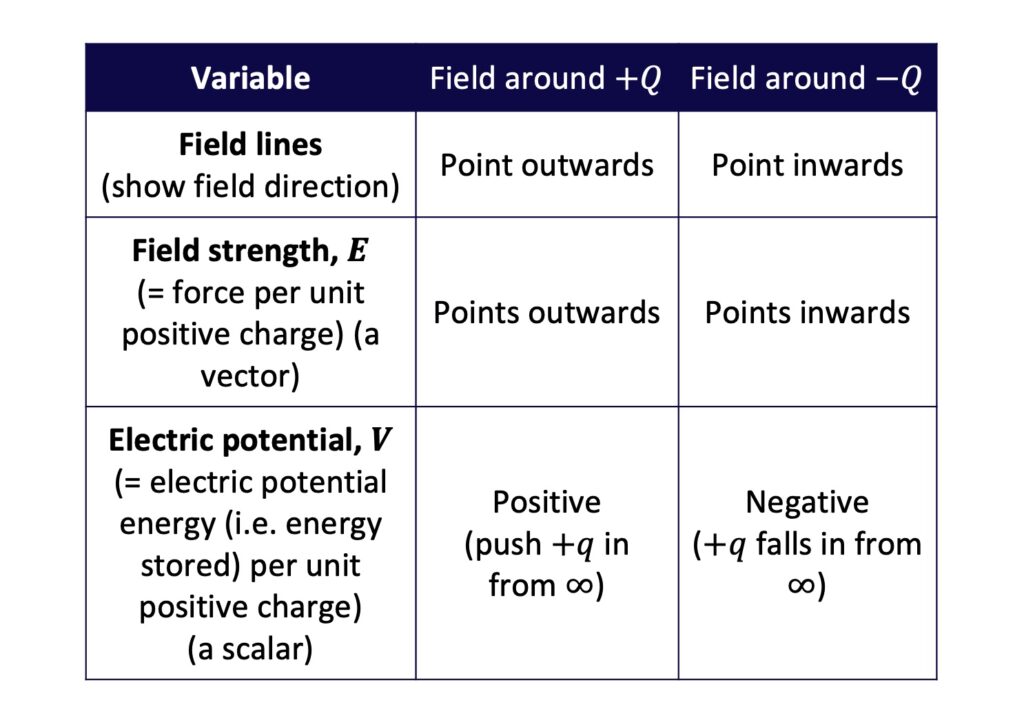
Electric fields around positive and negative charges
The sign of the charge \(Q\) at the centre of an electric field affects the directions and signs of various field properties.
Around positive \(Q\), field lines and field strength point outwards and electric potential is positive:
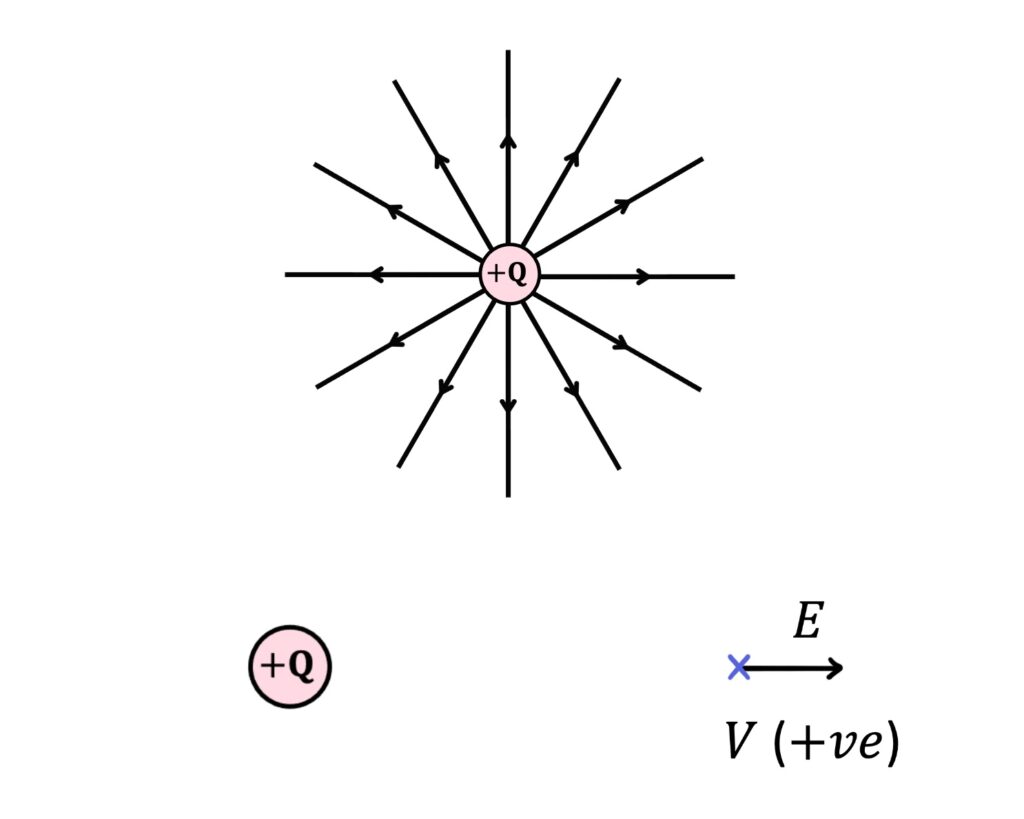
Around negative \(Q\), field lines and field strength point inwards and electric potential is negative:
These characteristics of fields around \(+Q\) and \(-Q\) are summarised in the following table.
How like and unlike charges interact
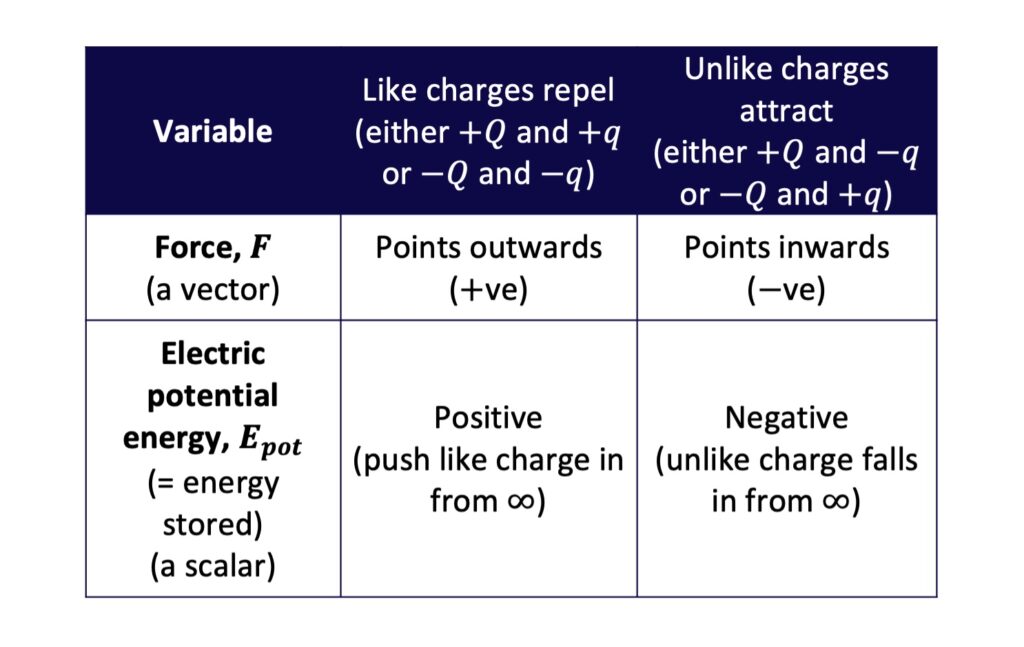
Like charges interact differently to unlike charges, and this also affects the sign of the electric potential energy of a charged object in a field.
If \(Q\) and \(q\) have the same sign, the electrostatic force points outwards (because like charges repel) and \(q\) has a positive potential energy:

If \(Q\) and \(q\) have different signs, the electrostatic force points inwards (because unlike charges attract) and \(q\) has a negative potential energy:

These factors are summarised in the following table.
Uniform electric fields
Until now, we have been considering the radial electric field around a point charge \(Q\). However, some electric fields are uniform, such as the field between two oppositely charged metallic plates:
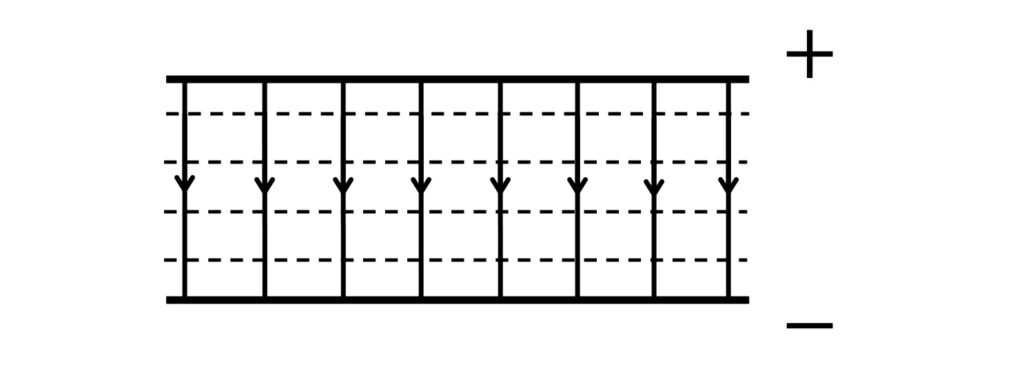
In a uniform electric field, the field lines are parallel (not radial) and the equipotentials are spaced at equal intervals. The equipotentials are equally spaced because the electric field strength \(E=-\frac{\Delta V}{\Delta r}\) is constant.
The force on a given charge \(q\) is also constant (because \(E\) is constant and \(F=qE\)). And since work done is force multiplied by distance, the work done to move a charge \(q\) by a distance \(r\) in a uniform electric field is \(\Delta W=F\times r=qEr\).
(This corresponds to the familiar \(\Delta W=mgh\) for work done raising a mass \(m\) by a height \(h\) in a uniform gravitational field of field strength \(g\).)
Conclusion
I hope you’ve enjoyed learning about electric fields!
We’ve covered a lot, from Coulomb’s law of electrostatics to some important properties of electric fields such as electric field strength and electric potential. We’ve also seen how the signs of charges affect field properties and interactions between charged objects.
If you haven’t done so already, you could take a look at the related topic of gravitational fields, or even compare gravitational fields and electric fields with each other.
Happy studying!
