Contents
Introduction
Electron diffraction provides evidence of the amazing wave-like characteristics that electrons can display. It therefore shows that electrons can behave both as particles and as waves!
In this post, we’re going to explore the theory of electron diffraction, and review the main experiments that demonstrate it to be true.
Let’s begin!
The de Broglie wavelength
The de Broglie wavelength is a wavelength assigned to all particles with mass. It represents the wave-like characteristics of these particles and is part of the overarching theory of wave-particle duality. According to wave-particle duality, waves can behave like particles and particles can behave like waves!
To derive an equation for the de Broglie wavelength, we need to start with the following two equations:
- Mass-energy equivalence: \(E=mc^2\)
- Energy of a photon: \(E=hf\)
Both of these equations are from Einstein’s miracle year of 1905 when he derived mass-energy equivalence (in his theory of special relativity) and he proposed an expression for the energy of a photon (in his explanation of the photoelectric effect). When explaining the photoelectric effect, he proposed that light came in discrete packets of energy called photons, and that these discrete packets gave electromagnetic waves particle-like characteristics.
Nineteen years later, de Broglie suggested that, conversely, particles with mass could behave like waves. He combined Einstein’s two equations above to bring mass (of particles) and frequency (of waves) together for the first time:
\(mc^2=hf\)
Since momentum is \(p=mc\) (where \(c\) is the particle’s speed) and the wave equation gives us \(c=\lambda f\), we can re-write this equation as:
\(pc=\frac{hc}{\lambda}\)
Cancelling \(c\) gives:
\(p=\frac{h}{\lambda}\)
And so the de Broglie wavelength is:
\(\lambda=\frac{h}{p}\)
This tiny equation has a big meaning! It tells us the wavelength exhibited by a particle of momentum \(p\).
Wavelength of an electron accelerated in an electric field
To investigate the wave-like nature of massive particles, it’s useful to create a beam of travelling electrons. The moving electrons have a de Broglie wavelength that depends on their momentum.
To create the beam, we can accelerate the electrons in an electric field through a potential difference of \(V\). Each electron in the beam then has a kinetic energy of:
\(\frac{1}{2}mv^2=eV\)
The de Broglie wavelength is:
\(\lambda=\frac{h}{p}=\frac{h}{mv}\)
And we can eliminate by rearranging \(\frac{1}{2}mv^2=eV\) for \(v\):
\(v=\sqrt{\frac{2eV}{m}}\)
Substituting this into the de Broglie wavelength, we get:
\(\lambda=\frac{h}{m \sqrt{\frac{2eV}{m}}}\)
And cancelling \(m\) gives:
\(\lambda=\frac{h}{\sqrt{2meV}}\)
You can see that the wavelength can be changed by adjusting the accelerating voltage, \(V\). This gives us the ability to “tune” the de Broglie wavelength of the moving electrons.
Experimental evidence of the wave nature of electrons
Now that we have our electron beam, we can shine it at various objects to make it diffract! The following experiments have been performed using electron beams to show their wave-like characteristics:
- Diffraction of electrons through a gap
- Two-slit electron interference
- Electron diffraction through a crystal
Electron diffraction through a gap
The simplest type of electron diffraction is diffraction through a gap. From wave theory, we know that for diffraction to happen the size of the gap needs to be comparable to the de Broglie wavelength:
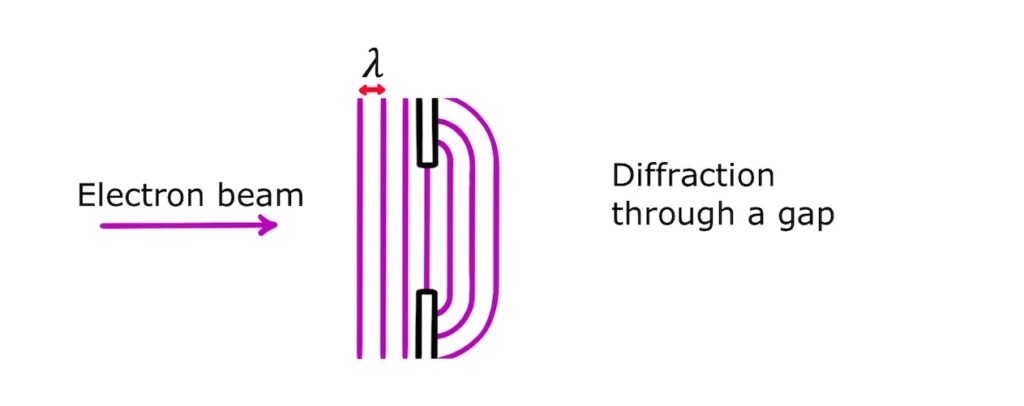
And maximum diffraction occurs when the gap width is equal to the de Broglie wavelength:

Electron diffraction experiments provide conclusive evidence that electrons have wave-like properties.
Two-slit electron interference
An electron beam can also be directed at a barrier having two gaps, each gap being the same size as the de Broglie wavelength. This produces two diffracting wavefronts that interfere with each other!
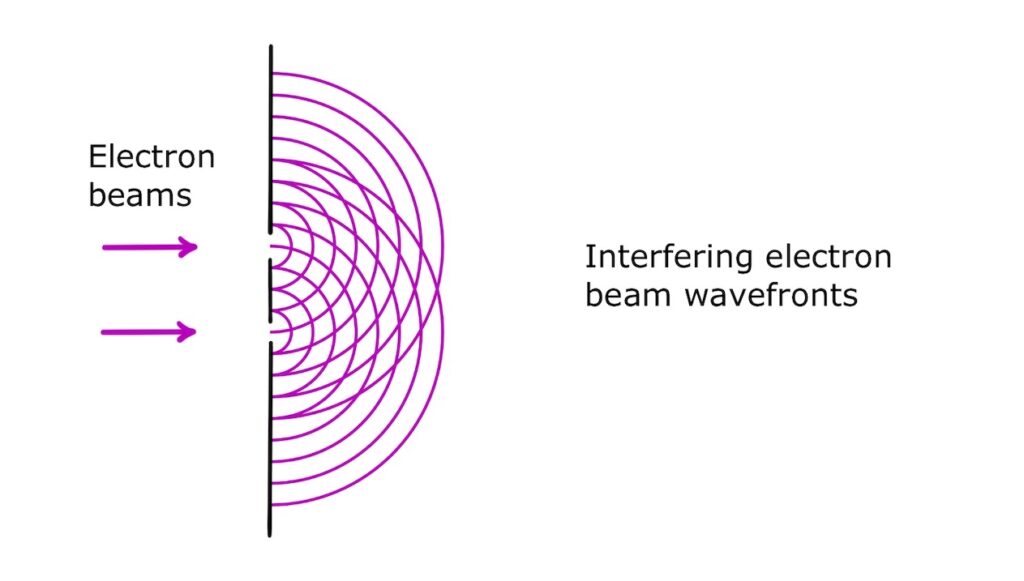
If we place a fluorescent screen after the gaps, we can detect the total intensity of the interfering waves.
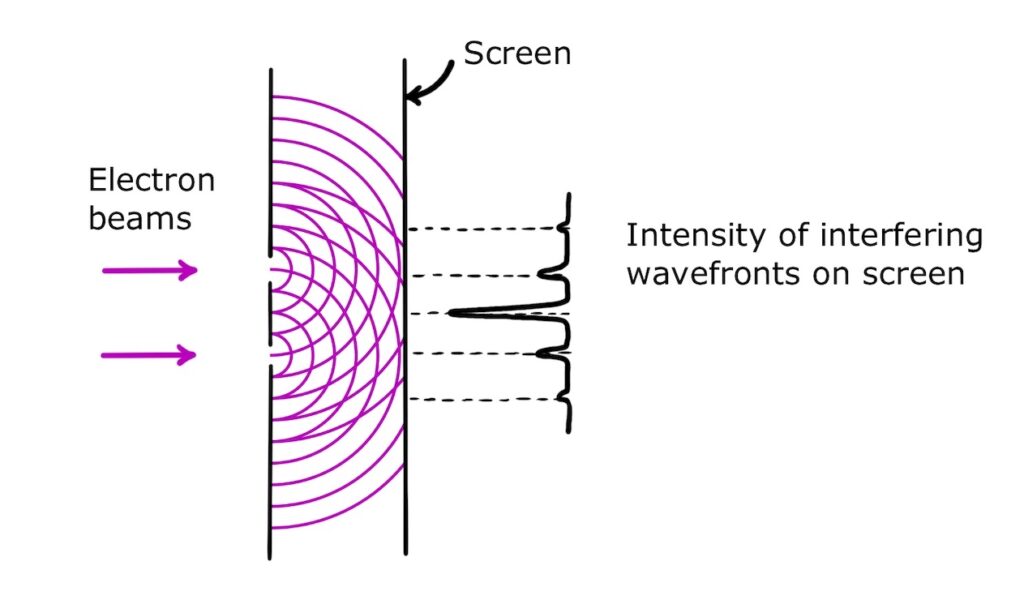
Looking straight at the screen, the total intensity will appear as a classic diffraction pattern consisting of a bright central area (or ‘central fringe’), with circular rings (‘outer fringes’) of decreasing intensity.

Two-slit interference has even been shown using an electron gun that fires one electron at a time. After a large number of electrons have been detected, an interference pattern builds up.
Since the electrons are fired one at a time, they cannot be interfering with each other—rather, each electron is interfering with itself! This implies that each electron passes through both slits (like a wave), which is incompatible with classical particle theory because a classical particle cannot pass through two slits at the same time.
Electron diffraction through a crystal
Finally, electron diffraction has also been demonstrated through crystals!
Crystals are repeating structures of atoms, so a very thin slice of a crystal contains rows of atoms which can act as a diffraction grating. It is the gaps between the atoms through which the electrons diffract.

The diffraction pattern is very similar to the two-slit interference pattern above. However, it will only be produced if the gaps between the atoms are comparable in size to the de Broglie wavelength of the electrons.
The de Broglie wavelength can, however, be tuned by changing the accelerating voltage of the electron gun. When a diffraction pattern is observed, the de Broglie wavelength is equal to the atom spacing, so this method can be used to investigate atom spacing in crystals.
Conclusion
I hope you’ve enjoyed learning about electron diffraction! This fascinating topic can be studied alongside the photoelectric effect and the overall topic of wave-particle duality.
Happy studying!
