Contents
Introduction
Force-extension graphs can tell us a lot about objects. When subjected to a stretching force, some objects simply stretch in proportion to the force applied, while others fracture or permanently change shape.
In this post, we’re going to explore a range of objects and their responses to stretching and compressing forces.
Let’s begin!
Extension and compression of a spring
A force can be applied to a spring so that it becomes extended or compressed compared to its original length.
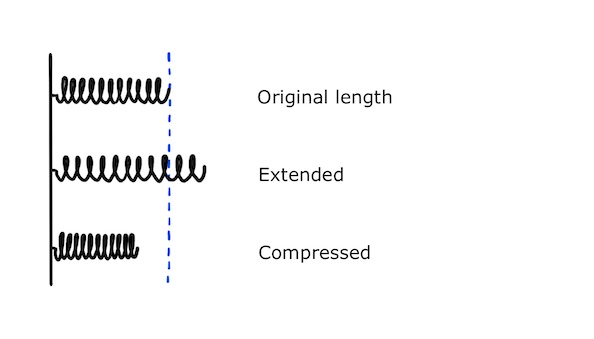
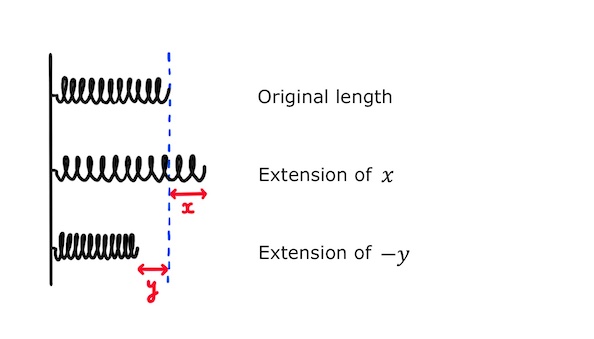
The amount by which it is extended is called its extension. If it becomes longer it has a positive extension and if it becomes shorter it has a negative extension.
The stretching and compressing forces are called tensile and compressive forces.
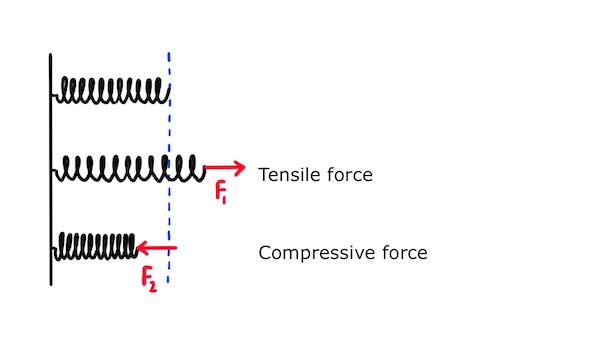
It’s important to note that the other end of the spring is attached to a fixed wall or other fixed object. Otherwise, the spring would be free and the applied force would accelerate it!
When a tensile force is applied to the spring, the spring in turn pulls on the wall, and (according to Newton’s third law of motion) the wall exerts an equal and opposite reaction force on the spring. As a result, when the spring is stretched there is a pair of equal and opposite tensile forces acting on it.
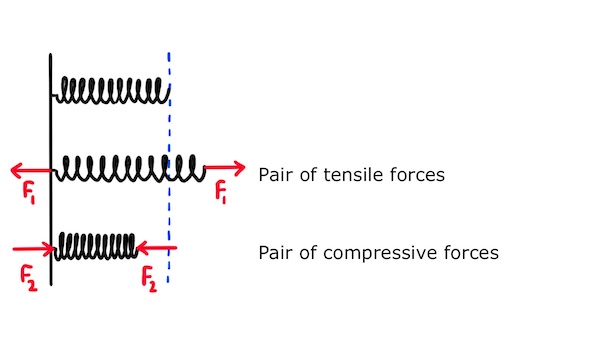
For similar reasons, when the spring is compressed there is a pair of equal and opposite compressive forces acting on it.
Hooke's law
Springs obey Hooke’s law which states that the extension of an object is proportional to the force applied.
This is expressed by the equation:
\(F=kx\)
where \(F\) is the force applied in Newtons, \(x\) is the spring’s extension in metres, and \(k\) is the spring constant of the spring, with units of \(\mathrm{Nm^{-1}}\). The spring constant is a measure of how stiff the spring is.
Plotting force against extension for the spring, we get a straight line with the gradient being equal to the spring constant.

Stiffer springs require more force for the same extension, so their force-extension graphs have steeper gradients and their spring constants are larger.
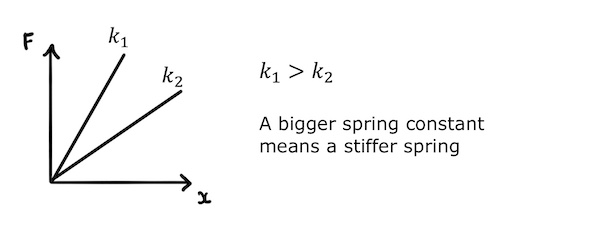
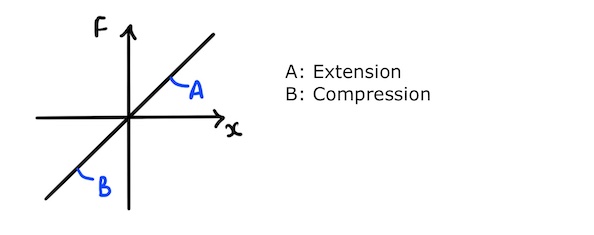
Hooke’s law can apply to both extension and compression. This means the straight line on a force-extension graph can extend into the negative \(x\) region, representing compression (B):
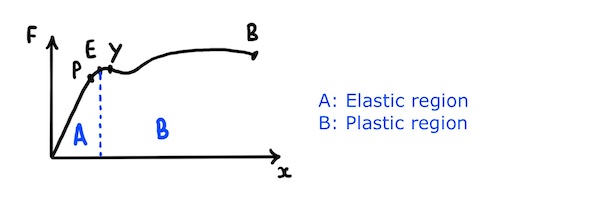
Elastic and plastic deformation
Another important concept in the mechanical properties of objects is the difference between elastic and plastic deformation.
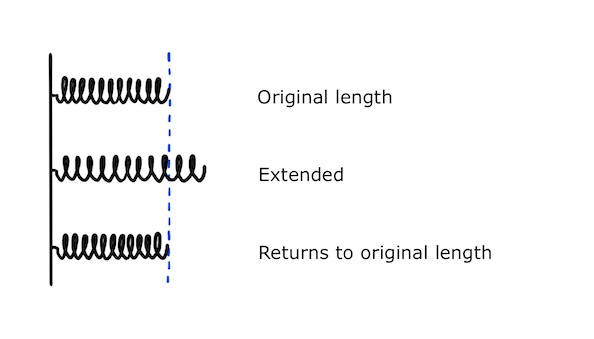
When an object is deformed in such a way that it returns to its original shape when the force is removed, it is said to have deformed elastically.
For example, if a spring is extended by a short extension, it will deform elastically and return to its original shape when the force is removed.
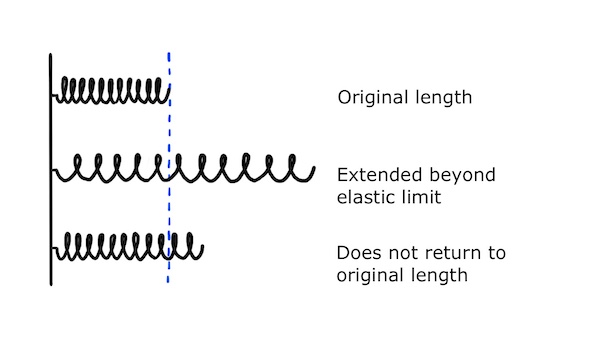
However, if the spring is stretched too far (beyond its elastic limit), it will undergo plastic, or permanent, deformation and will not return to its original shape.
Elastic and plastic deformation have a wide range of applications in engineering. For example, crumple zones in cars deform plastically to absorb shock.
Meanwhile, components in the foundations of earthquake-proof buildings deform elastically to provide some flexibility. This makes the foundations less rigid and less prone to breakage which could otherwise make the building more likely to collapse.
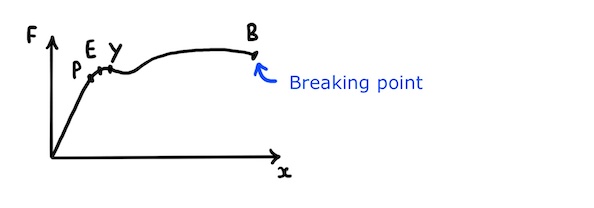
Extension of a typical metal wire
Let’s take what we’ve learnt from springs and apply this to some other interesting objects.
For example, a typical metal wire has a force-extension graph that looks like this:
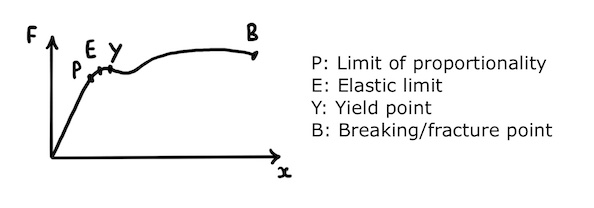
The key features are:
- The limit of proportionality, \(P\)
- The elastic limit, \(E\)
- The yield point, \(Y\)
- The fracture or breaking point, \(B\)
As we can see, the metal wire’s extension is proportional to the force applied up to its limit of proportionality, \(P\). As such, the wire obeys Hooke’s law up to point \(P\).
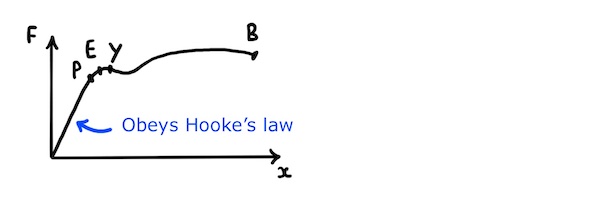
In this region of proportionality, bonds between the metal’s atoms behave like tiny springs that extend in accordance with Hooke’s law as the wire stretches.
The bonds store elastic potential energy when they are stretched and will return the wire to its original length when the force is removed, provided the wire is not stretched beyond its elastic limit, \(E\).
Beyond the elastic limit, the wire enters the plastic region where further extension takes place by atoms moving around and relocating with respect to each other. This does not produce restorative forces from stretched bonds, so when the tensile force is removed the wire does not return to its original length.
After the atoms have reorganised themselves a little, they can move more easily and, just after the yield point, \(Y\), it becomes easy to stretch the wire.
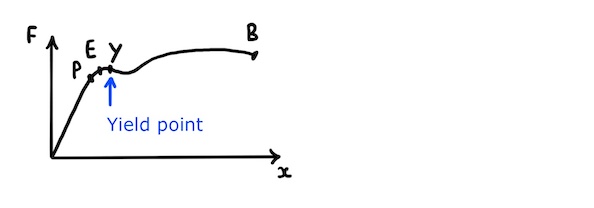
The wire continues to extend plastically after the yield point until it breaks.
Extension of a brittle object
Brittle objects, such as those made of glass or ceramics, obey Hooke’s law and undergo very small extensions before breaking.
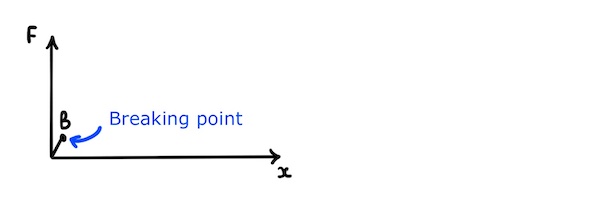
This is a result of a rigid atomic structure. The atoms are strongly bonded to their neighbours to form a giant lattice in which they cannot move with respect to each other. After a small extension from stretching the atomic bonds, the rigid structure breaks and the object fractures.
Elastic behaviour of a rubber band
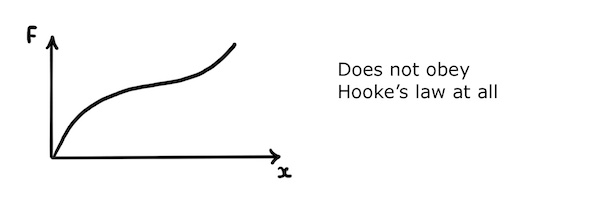
A rubber band is very different to a brittle object. It stretches a lot before breaking and does not obey Hooke’s law at all!
Its elastic limit is beyond its breaking point, so until it breaks it will always stretch elastically and return to its original shape.
As we can see from the changing gradient of the force-extension graph, the rubber band is initially stiff, then less stiff, and then stiff again.
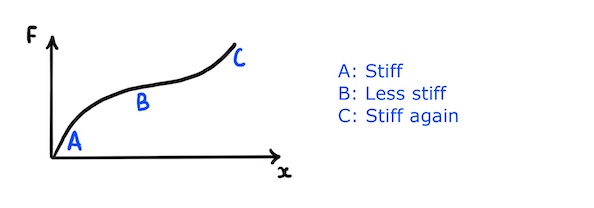
This intriguing behaviour is because rubber consists of polymers which are long molecules made up of large numbers of atoms. The long polymers are naturally tangled up with each other in a disorganised way like tangled wires. As a result, it takes a fair amount of force to untangle them and stretch them out.
After some initial stretching, the polymers are less tangled and it becomes easier to stretch them out. The rubber band therefore becomes less stiff.
Eventually, the polymers are so stretched that they become almost linear and any further extension is only possible by stretching their atomic bonds. This requires more force, so the rubber band becomes stiff again.
Conclusion
I hope you’ve enjoyed learning about the responses of objects to tensile and compressive forces!
Insights into their atomic structure can explain a lot about their behaviour and help you understand the meaning behind their force-extension graphs.
