Contents
Introduction
Understanding what electricity is and where it comes from can make it much easier to grasp electrical concepts and remember the relationships between electrical quantities.
In this post, we’re going to explore the fundamentals of electricity so you’re off to a great start in this exciting topic.
Let’s begin!
How cells supply electricity
Electrochemical cells supply electricity to circuits by converting stored chemical energy into electrical energy.
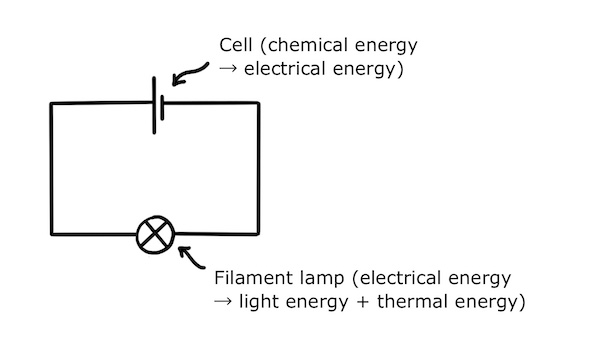
Chemicals in the cell have a high chemical potential energy. They want to get rid of some of this energy to achieve a more stable, lower energy state. Some of them can do this by releasing electrons and others can do it by accepting electrons.
The electron donors and acceptors are at different terminals of the cell. The electron donors release their unwanted electrons to their terminal, making it negative. And the electron acceptors “steal” electrons from their terminal, making it positive.
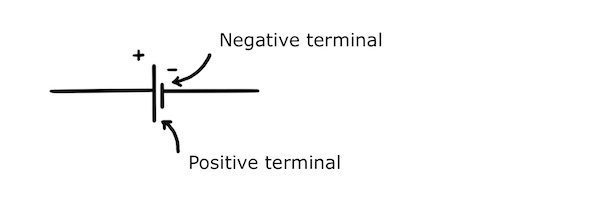
If the cell is connected to a complete circuit, the excess electrons that have accumulated at the negative terminal will be able to flow around the circuit to the positive terminal. And there we have it: this flow is electrical current!

The current will continue to flow around the circuit until the available chemical energy in the cell has run out and the energy conversion process is complete.
Electromotive force of a cell
The emf, \(\epsilon\), of a cell is the amount of chemical energy it converts into electrical energy per unit of charge that flows. It can be thought of as how much energy the cell gives the electrons as they travel off into the circuit.
It can be expressed as:
\(\epsilon=\frac{W}{Q}\)
where \(W\) is the work done in joules, \(\mathrm{J}\), by the cell converting chemical energy into electrical energy and \(Q\) is the amount of charge passing in Coulombs, \(\mathrm{C}\).
Emf has units of \(\mathrm{JC^{-1}}\) which is the volt, \(\mathrm{V}\), so emf is often also referred to as the cell’s voltage.
Electric current
Electric current is the rate at which charge flows:
\(I=\frac{Q}{t}\)
where \(Q\) is the charge passing in Coulombs, \(\mathrm{C}\), and \(t\) is the time for the charge to pass in seconds, \(\mathrm{s}\).
Current has units of Amperes, \(\mathrm{A}\), or ‘Amps’ for short.
The above equation is often rearranged to \(Q=It\), which is easy to remember and can be helpful for calculating the charge passing in time \(t\).
One thing to watch out for is the direction of conventional current. It is from positive to negative even though electrons flow in the opposite direction.

This is because when scientists first discovered electricity, they didn’t know it was caused by moving electrons and thought there might be a positive charge carrier. So they proposed that current flows from positive to negative, a convention we still use today.
Conduction in metals
The chemistry of metal atoms means that they are more stable if they give up one or more of their electrons to become positively charged ‘ions’. The atomic structure of a metal is therefore a lattice of positively charged ions surrounded by a sea of electrons that are free to move around.
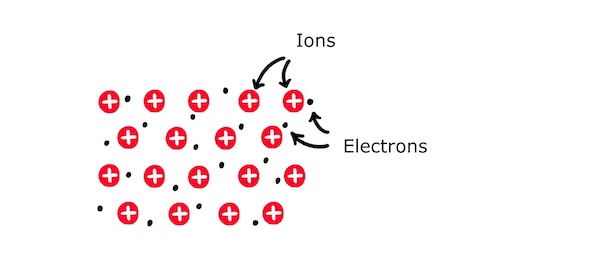
The electrons move around rapidly due to the thermal energy of the metal, colliding frequently with the ions.
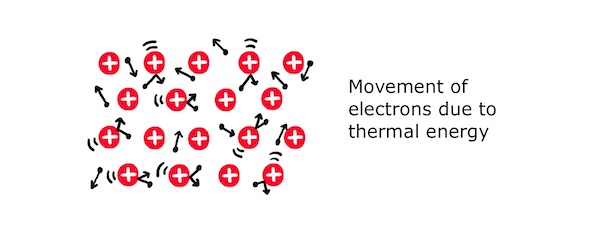
When the metal is connected to a cell, the free electrons are attracted to the positive terminal and, despite frequent collisions with the ions, they drift slowly towards the positive terminal. It is this drift that is the electric current.
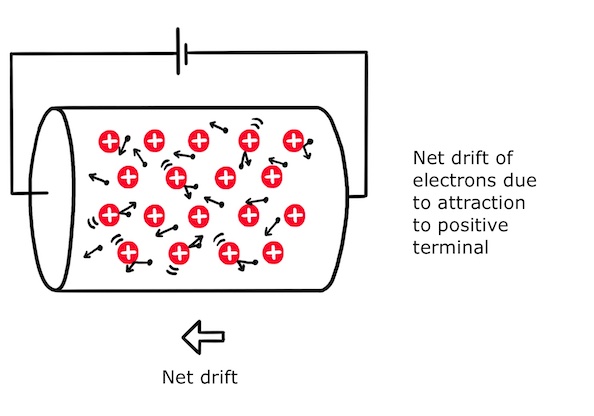
Drift velocity and the transport equation
The rate at which electrons drift is called the drift velocity.
We can model conduction in metals as the flow of tiny, positive charge carriers travelling in the direction of conventional current.

If the charge carriers travel a distance \(\Delta x\) in time \(\Delta t\), the drift velocity can be expressed as:
\(v=\frac{\Delta x}{\Delta t}\)
In time \(\Delta t\), all the charge carriers in volume \(V=A\Delta x\) will travel past the end of the volume.
There are \(N=nV\) charge carriers in volume \(V\), where \(n\) is the density of charge carriers in the metal.
Since each charge carrier carries a charge of \(q\), the total charge passing is:
\(\Delta Q=Nq=nVq=nA\Delta xq\)
Dividing both sides by \(\Delta t\), we have
\(\frac{\Delta Q}{\Delta t}=\frac{nA\Delta xq}{\Delta t}\)
But \(I=\frac{\Delta Q}{\Delta t}\) and \(v=\frac{\Delta x}{\Delta t}\), so
\(I=nAvq\)
This is the transport equation! It relates drift velocity to quantities we can either measure or look up.
Potential difference across a circuit component
The potential difference, \(V\), or ‘pd’ between two points in a circuit is the amount of electrical energy converted into other forms of energy per unit of charge passing.
The pd across a circuit component is therefore the work done by the circuit component per unit of charge passing:
\(V=\frac{W}{Q}\)
where \(W\) is the work done in joules, \(\mathrm{J}\), and \(Q\) is the charge passing in Coulombs, \(\mathrm{C}\).
The pd across a circuit component can also be thought of as the electrical energy the component extracts from each Coulomb of charge that flows through it.
Like emf, pd has units of \(\mathrm{JC^{-1}}\) which is the volt, \(\mathrm{V}\). The pd across a component is therefore also sometimes referred to as the voltage across the component.
Work done by a circuit component
It follows easily from this that the work done by a circuit component is the charge passing through it multiplied by the pd across it:
\(W=QV\)
Since \(Q=It\), the work done by a circuit component can also be expressed as:
\(W=VIt\)
where \(V\) is the pd across it, \(I\) is the current flowing through it and \(t\) is the time for which the current flows.
Resistance
As we saw above, when a current flows through a wire, electrons frequently collide with ions. These collisions create resistance which is the opposition of an object to the flow of electrical current.
The electrical resistance of an object is defined as the pd required to cause a unit of current to flow. Therefore we have:
\(R=\frac{V}{I}\)
where \(V\) is the pd across the object in volts, \(\mathrm{V}\), and \(I\) is the current flowing through it in Amps, \(\mathrm{A}\). This rearranges to \(V=IR\).
Resistance has units of \(\mathrm{VA^{-1}}\), the Ohm, \(\mathrm{\Omega}\).
It’s important to note that although metal wires have resistance, this is negligible compared to the resistance of a typical circuit component. As a result, you can ignore the resistance of the wire in a circuit!
Since \(V=IR\) and \(I>0\), the approximation \(R=0\) also implies \(V=0\). So the pd across a wire in a circuit can also be ignored.
Conclusion
I hope you’ve enjoyed learning about the fundamentals of electricity!
Armed with this knowledge, you can now answer a whole range of questions about electricity and tackle the more advanced topics of circuit components and complete electrical circuits with confidence.
