Contents
Introduction
The photoelectric effect is an interesting phenomenon that can only be explained by considering light as particles, not as waves. It therefore demonstrates the particle nature of light and played an important role in early quantum theory.
In this post, we’re going to explore the photoelectric effect, its far reaching implications, and how it can be demonstrated experimentally using the gold leaf and photocell experiments.
Let’s begin!
What is the photoelectric effect?
The photoelectric effect is the emission of electrons from the surface of a metal when it is irradiated with electromagnetic radiation.

Metals are made up of positive ions (atoms with one or more electrons removed) surrounded by a sea of the removed electrons, which are called conduction band electrons and are free to move around the metal. It is these conduction band electrons that are emitted from the metal in the photoelectric effect.
If a conduction band electron absorbs an incident photon having energy \(E=hf\) and the energy is enough to overcome the electron’s attraction to the metal ions, the electron can be removed from the metal. Any left over energy is converted into kinetic energy, \(KE\), with which the electron escapes. Electrons escaping in this way are known as photoelectrons.
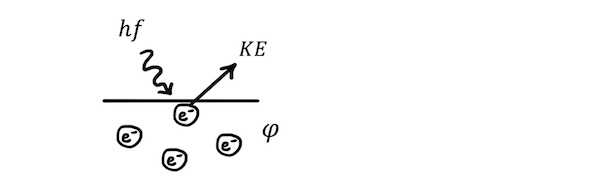
The amount of energy required to remove an electron from the surface of the metal is called the work function, \(\phi\), of the metal. As a result, when a photon removes an electron from the surface of a metal, all its energy beyond the work function is converted into kinetic energy, and the photoelectron leaves with the maximum kinetic energy.
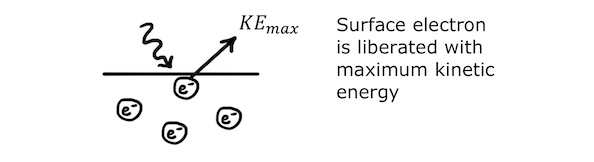
It takes a bit more energy to remove an electron from just below the surface, so slightly less of the photon’s energy is left over as kinetic energy. Electrons removed from below the surface leave with less kinetic energy than surface electrons.
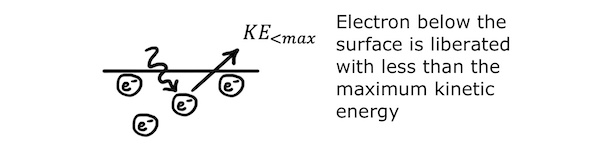
As a result of the additional energy required to remove an electron from below the surface, photoelectrons are emitted with a range of kinetic energies depending on how close they are to the surface of the metal.
The photoelectric effect equation
If we consider a photoelectron emitted from the surface, it is emitted with the maximum kinetic energy, which is the photon energy, \(hf\), minus the work function of the metal, \(\phi\).
This is summed up nicely in Einstein’s photoelectric effect equation:
\(KE_{max}=hf-\phi\)
Since \(KE_{max}=\frac{1}{2}m{v_{max}}^2\), we can also express this as:
\(\frac{1}{2}mv_{max}^2=hf-\phi\)
We will revisit this equation later in graphical form when we explore the photocell experiment 🙂
What is the threshold frequency in the photoelectric effect?
Photoelectrons are only emitted if each incoming photon has enough energy to remove an electron from at least the surface of the metal.
This means that the photon energy, \(hf\), needs to be at least equal to the work function, \(\phi\), of the metal and that there is a threshold frequency, \(f_0\), above which the photoelectric effect will be observed:
\(hf_0=\phi\)
If a photon with a frequency below the threshold frequency is absorbed by a surface electron, it will not have enough energy to remove the electron. Instead, the electron will vibrate and the photon’s energy will be dissipated into the metal as heat.
The photoelectric effect as evidence of the particle nature of light
The threshold frequency is important because it means that the photoelectric effect cannot be explained by the wave model of light.
Thinking of light as a wave, we would expect to observe the photoelectric effect even with low frequencies of electromagnetic radiation because the wave energy should build up if we shine it for long enough or with sufficient intensity.
But this is not what happens. If the frequency is too low no photoelectrons are emitted, no matter how long or how intensely we shine the light for!
We must conclude, therefore, that light is delivered in discrete packets or ‘quanta’ of energy (called photons) and that electrons in the metal absorb one photon at a time. If a photon arrives with sufficient energy it can remove an electron, but if its frequency is too low it cannot.
This provides compelling evidence of the particle nature of light, and shows that there are circumstances in which light behaves as a particle and not as a wave.
Demonstrating the photoelectric effect using the gold leaf experiment
The photoelectric effect can be demonstrated experimentally using an electroscope having a zinc plate, a zinc stalk and a gold leaf attached to the stalk.
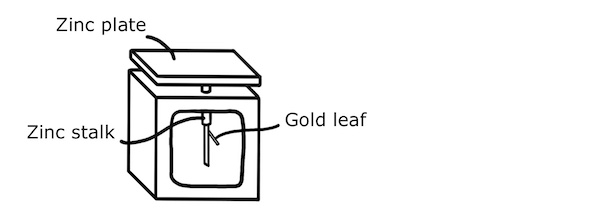
At the start of the experiment, the plate is charged with an excess of electrons so that the stalk deflects the gold leaf by electrostatic repulsion.
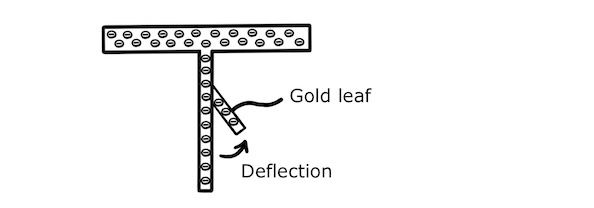
If we irradiate the zinc plate with ultraviolet radiation and cause it to emit photoelectrons by the photoelectric effect, it will discharge and there will no longer be electrostatic repulsion between the stalk and the gold leaf. We therefore expect the gold leaf to fall when the photoelectric effect takes place.
When the zinc plate is illuminated with light of different frequencies and intensities, we see some interesting results:
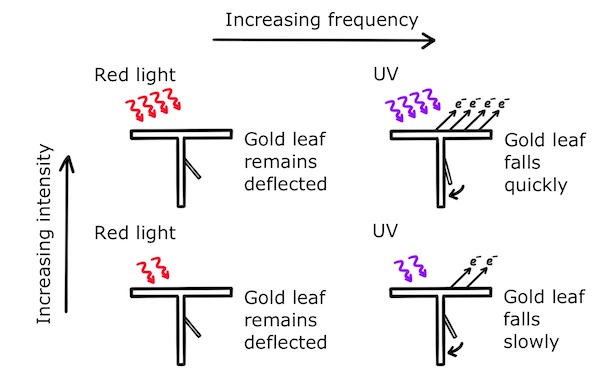
We observe that:
- The gold leaf only falls when the light is above a threshold frequency
- For light above the threshold frequency, increasing the intensity makes the gold leaf fall faster
- For light below the threshold frequency, increasing the intensity does not make the gold leaf fall
We can explain these observations using a particle model of light:
- The zinc plate discharges only when each photon has at least enough energy to remove a surface electron
- Electrons cannot absorb multiple lower energy photons until they have enough energy to escape: they can absorb only one photon at a time
- When the photons have enough energy to remove electrons, increasing the intensity causes more photoelectrons to be emitted per second, and the zinc plate discharges faster
If we were also to measure the kinetic energies with which the photoelectrons are emitted, we would find that the maximum kinetic energy increases with the frequency of the light. This is consistent with the idea that electrons absorb one photon at a time and if the photon energy goes up, the photoelectrons can leave with more kinetic energy.
Since the above observations can only be explained by thinking of light as particles, and not waves, the gold leaf experiment demonstrates the particle nature of light.
Measuring stopping potential in the photocell experiment
We can also observe the photoelectric effect in a more quantitative way using the photocell experiment.
The idea is to emit photoelectrons from a metal plate and make them climb a small electric potential using their kinetic energy to reach another metal plate. If we gradually increase the electric potential between the plates, we make it harder for the photoelectrons to cross the gap. Eventually, the energy required for the photoelectrons to make it across the gap will be equal to their maximum kinetic energy and if we increase the electric potential any further, no photoelectrons will make it across. This gives us a way of determining their maximum kinetic energy.
The energy required for a photoelectron to cross the gap is its charge, \(e\), multiplied by the potential difference, \(V\), between the plates — i.e. \(E=eV\).
If we gradually increase the potential difference to the point where it stops photoelectrons crossing the gap, we will have reached the point where the energy required to cross the gap is equal to the maximum kinetic energy. The potential difference at this point is called the stopping potential, \(V_s\), and it allows us to calculate the maximum kinetic energy from \(eV_{s}=KE_{max}\).
To set this up experimentally, we connect two metal plates to a variable power supply to create a positively charged anode and a negatively charged cathode.
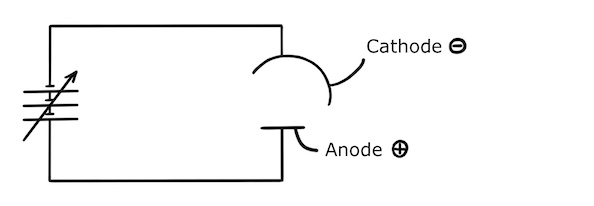
The anode and cathode are enclosed in a box containing a vacuum and we shine light on the anode. (The vacuum ensures that photoelectrons travelling between the anode and the cathode are not scattered by gaseous molecules on the way.)

If the frequency of the light is sufficiently high, the photons will have enough energy to remove electrons from the anode and give them enough kinetic energy to make it across to the cathode. Since the photoelectrons will then be travelling across the gap, this will set up a small current in the circuit which can be measured using a micrometer!
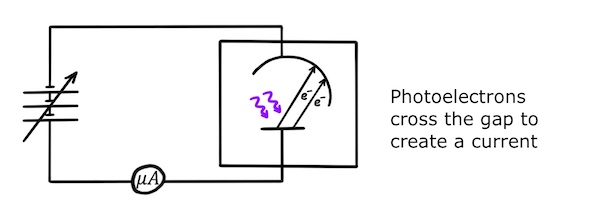
Now we are going to make it harder for the photoelectrons to cross the gap. If we gradually increase the voltage of the variable power supply, the potential difference between the anode and the cathode will increase until eventually it reaches the stopping potential, \(V_s\), and stops the current from flowing.
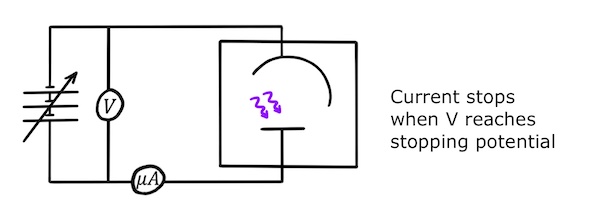
By measuring the stopping potential, we can determine the maximum kinetic energy:
\(eV_s=\frac{1}{2}m{v_{max}}^2\)
Repeating this for multiple frequencies of light, we can plot the maximum kinetic energy against frequency:
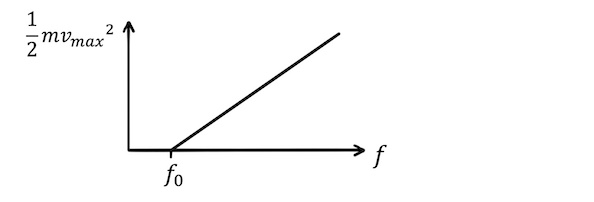
We can see that the photoelectric effect takes place for frequencies above a threshold frequency, \(f_0\), and that increasing the frequency above this threshold increases the kinetic energy of the photoelectrons.
By relating this graph to Einstein’s photoelectric effect equation,
\(\frac{1}{2}m{v_{max}}^2=hf-\phi\),
we can reveal that the gradient of the graph is Plank’s constant and the y-intercept is minus the work function of the anode.

The photocell experiment therefore enables us to determine the threshold frequency, Plank’s constant, the maximum kinetic energy of the photoelectrons, and the work function of the metal using a straightforward experimental setup.
Conclusion
The photoelectric effect is an important phenomenon that provides evidence of the particle nature of light. It can be demonstrated using simple experiments that show profound results.
Since light can also behave as a wave, it has both wave and particle characteristics. Wave-particle duality is an exciting phenomenon that is widespread in nature and exhibited not only by light but also by other particles.
