Contents
Introduction
Mechanics is a fascinating topic concerning the motion of objects and their interactions via forces.
In this post, we’re going to review the principles of mechanics so you have a strong grasp of the foundations of this topic.
Let’s begin!
Kinematics equations
The kinematics equations— also known as the equations of motion—describe the movement of objects. Together, they describe the relationships between the following properties:
- Displacement, \(s \,(\mathrm{m})\)
- Initial velocity, \(u \,(\mathrm{ms^{-1}})\)
- Final velocity, \(v \,(\mathrm{ms^{-1}})\)
- Acceleration, \(a \,(\mathrm{ms^{-2}})\)
There are four equations of motion, and we’re going to derive them now for the case of uniform acceleration.
For an object moving with uniform acceleration, velocity increases by \(at\) in time \(t\). The object’s final velocity is therefore its initial velocity plus \(at\). This gives us the first equation of motion!
\(v=u+at\)
The displacement travelled during time \(t\) is the average velocity multiplied by time. Since acceleration is constant, the average velocity is \(\frac{1}{2}(u+v)\). So the displacement is:
\(s=(\frac{u+v}{2})t\)
Two down, two to go!
Let’s substitute \(v\) from the first equation into the second equation to get another expression for displacement:
\(s=(\frac{u+u+at}{2})t\)
\(=\frac{2ut+at^2}{2}\)
\(=ut+\frac{1}{2}at^2\)
This gives us the third equation of motion:
\(s=ut+\frac{1}{2}at^2\)
Finally, let’s find an equation without \(t\). To achieve this, we can rearrange the second equation of motion for \(t\), and substitute this expression into the first equation of motion. Rearranging \(s=(\frac{u+v}{2})t\) for \(t\) gives:
\(t=\frac{2s}{u+v}\)
Substituting this into \(v=u+at\) gives:
\(v=u+a(\frac{2s}{u+v})\)
\(\implies(v-u)(u+v)=2as\)
\(\implies vu+v^2-u^2-uv=2as\)
This gives us our fourth and final equation of motion:
\(v^2=u^2-2as\)
Newton’s 1st and 2nd laws of motion
Newton’s first and second laws of motion tell us about how an object’s motion is affected by a resultant force acting on the object.
Newton’s first law of motion states that:
An object will remain in a state of uniform motion or rest until acted on by a resultant force.
In other words, if there is no resultant force acting on the object, its motion will continue at a constant velocity.
Newton’s second law of motion states that:
The resultant force acting on an object is equal to the object’s mass multiplied by its acceleration.
This is our familiar friend, \(F=ma\)!
In fact, Newton’s first law is really a sub-category of the second law in the case when the resultant force is zero. (When \(F=0\), \(a=0\), and the object’s velocity remains constant).
Newton’s 3rd law of motion
Newton’s third law of motion is a bit different. It states that:
When a first object causes a force on a second object, the second object causes an equal and opposite reaction force on the first object.
Thus, when we talk about Newton’s third law, we are talking about two objects exerting forces on each other. These forces are sometimes called Newton pairs of forces.
We need to be careful when identifying Newton pairs of forces. Remember, the forces act on different objects.
For example, don’t get confused with weight and a normal force acting on the same object. These are equal and opposite, but they are not a Newton pair!

The box’s weight is due to its gravitational attraction to a second object, the Earth. Therefore, there is an equal and opposite gravitational attraction exerted by the box on the Earth. Together, the two gravitational forces form a Newton pair:
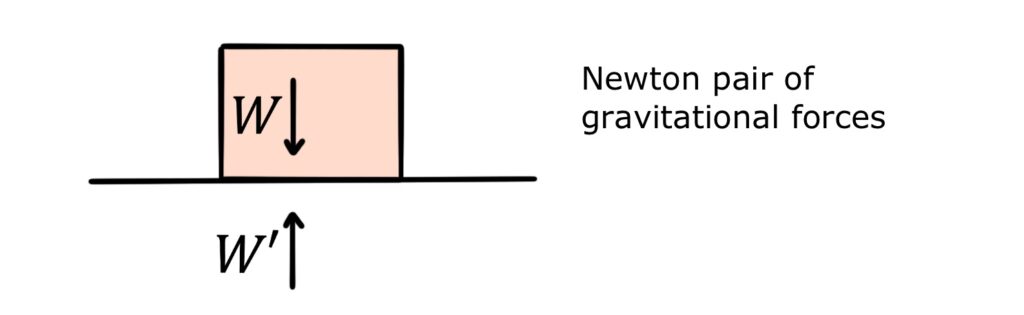
Similarly, the normal force supporting the box is a contact force arising from electrons at the edge of the surface electrostatically repelling electrons at the edge of the box. There is an equal and opposite contact force exerted electrostatically by the box on the Earth. These two contact forces form another Newton pair:
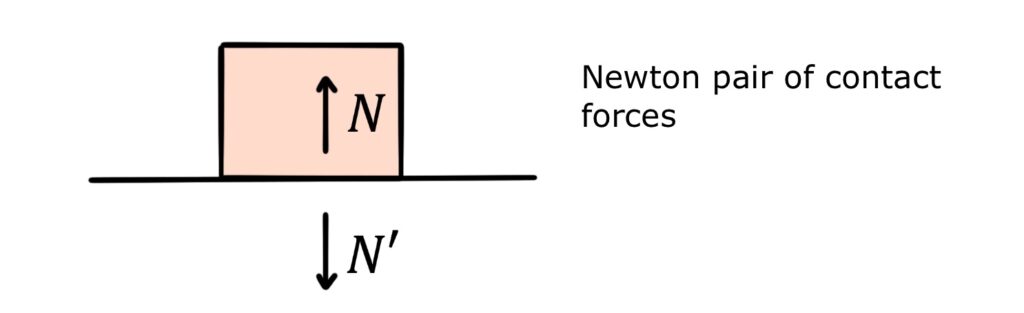
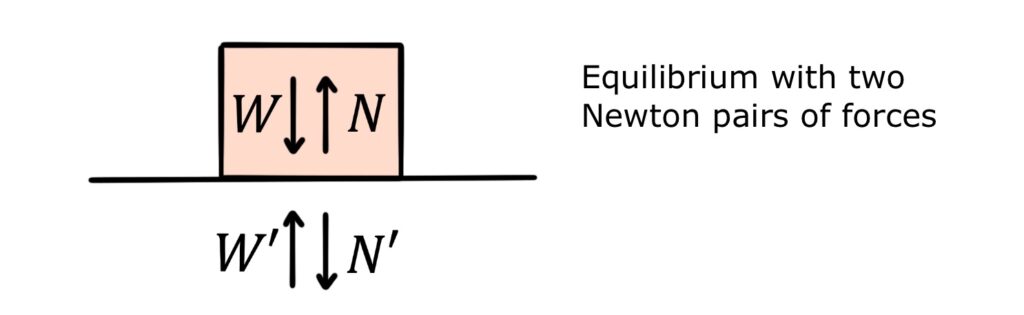
Since the box is stationary, the system is in equilibrium and the resultant force on each object is zero:
\(F_{box}=W+N=0\)
\(F_{earth}=W’+N’=0\)
Conservation of momentum
The conservation of momentum is an important fundamental principle in physics. It states that in the absence of external forces the total momentum of a system is conserved.
This principle is often applied in the context of explosions and collisions.
It has a special relationship with Newton’s third law of motion. In fact, the conservation of momentum is implied by Newton’s third law!
Starting with Newton’s third law, we know that interacting objects exert equal and opposite forces on each other (\(+F\) and \(-F\)).
Since momentum is \(p=mv\), Newton’s second law (\(F=ma\)) can be expressed as follows:
\(F=m\frac{dv}{dt}\)
\(=\frac{dp}{dt}\)
So force is the rate of change of momentum:
\(F=\frac{dp}{dt}\)
If two interacting objects exert a pair of Newton forces \(+F\) and \(-F\) on each other during time \(\Delta t\), their changes in momentum are \(+\Delta p\) and \(-\Delta p\). The total change in momentum of the system is therefore zero, and momentum is conserved:
\(\Delta p_{total}=+\Delta p-\Delta p=0\)
Thus, Newton’s third law implies the conservation of momentum.
Work done
Finally, work done is the energy transferred to or from an object by a force acting on the object along a displacement.
\(work=force \times \, displacement\)
This force is the force that causes the displacement. It is not to be confused with the resultant force acting on the object (although it may be equal to the resultant force if there are no other forces acting).
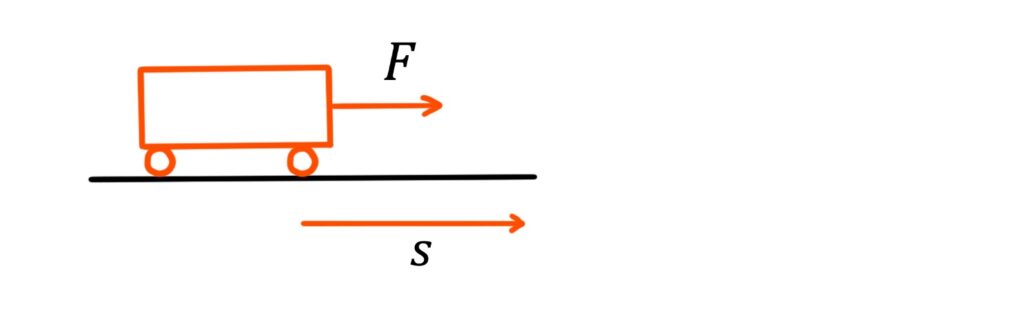
For example, the work done by force \(F\) pulling a trolley a displacement \(s\) is:
\(work=Fs\)
If the force is at an angle to the displacement, we need to resolve it in the direction of the displacement (because the force must be acting along the displacement):
\(work=Fscos\theta\)

All other forces on the trolley (such as friction, weight and air resistance) can be ignored. The only force you need to use when calculating the work done is the force that causes the displacement.
Summary
I’ve summarised the key takeaways from this post for you in the following image!

Conclusion
I hope you’ve enjoyed this review of some of the most fundamental and important principles of mechanics! Getting a really clear understanding of these principles will give you a solid foundation for solving a wide range of problems.
Armed with this knowledge, you might like to explore some other mechanics topics too, such as projectiles, collisions, power and efficiency, moments and rotational equilibrium, oscillations, and simple harmonic motion.
Happy studying!
