Contents
Introduction
The equations for radioactive decay provide us with a neat set of mathematical tools for describing nuclear decay processes.
In this post, we’re going to review the meanings and derivations of the radioactive decay equations and see how they look graphically.
Let’s begin!
Rate of radioactive decay
Radioactive decay is a random and spontaneous process by which unstable nuclei become more stable by transforming into a different, lower energy nucleus or into a lower energy state. They loose energy by emitting radiation such as alpha, beta and gamma radiation.
For a given radioactive nucleus, the rate of decay is a constant that depends its number of protons, its number of neutrons, and—in the case of gamma radiation—whether it is in an excited internal energy state. Importantly, the rate of decay is not influenced by environmental factors such as temperature and pressure. It is a genuinely random process, driven only by probabilities.
An important property of a radioactive nucleus is the decay constant, \(\lambda\), which is defined as the probability that the nucleus will decay in the next second.
The decay constant therefore tells us the portion of nuclei in a sample that will decay per second. For example, if \(\lambda=0.5\) for a given type of nucleus, half the nuclei in the sample will decay in the next second:
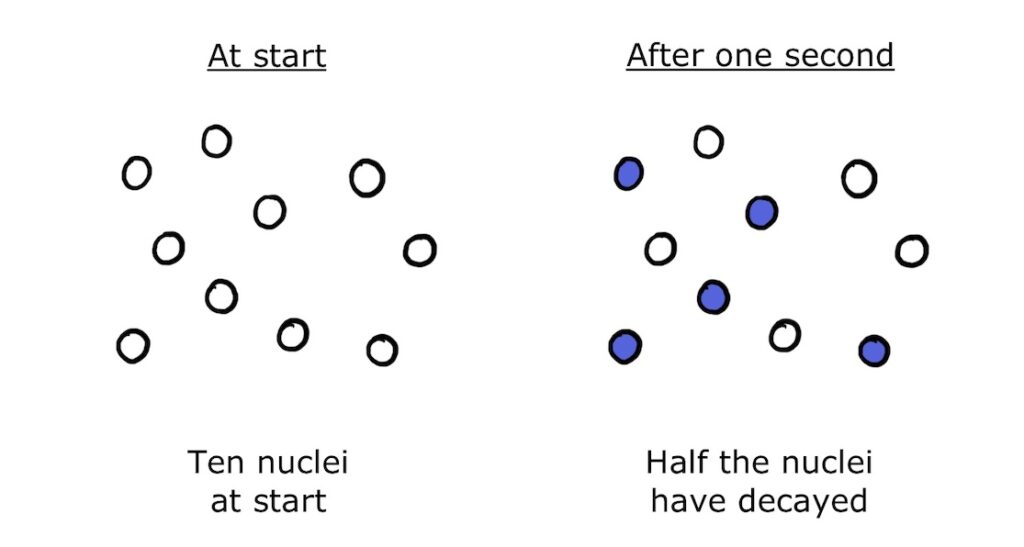
The actual number of nuclei that decay per second is the decay constant multiplied by the sample size: \(N\lambda\). This is the rate of decay, and the rate of change of the sample size is equal to minus the rate of decay:
\(\frac{dN}{dt}=-\lambda N\)
Radioactive activity
The rate of decay is also known as the activity, \(A\), of the sample. So we can define activity as follows:
\(A=\lambda N\)
And we can write:
\(\frac{dN}{dt}=-A\)
Exponential decay of radioactive substances
Radioactive substances decay exponentially, which can be shown by integrating \(\frac{dN}{dt}=-\lambda N\) from an initial number of nuclei, \(N_0\), to an arbitrary number of nuclei, \(N\), at time \(t\).
\(\int_{N_0}^{N}\frac{1}{N}dN=-\lambda \int_{0}^{t}dt\)
\(\left[lnN\right]_{N_0}^N=-\lambda\left[t\right]_0^t\)
\(lnN-lnN_0=-\lambda(t-0)\)
\(ln{\frac{N}{N_0}}=-\lambda t\)
This derivation gives us an important expression for the sample size at time \(t\):
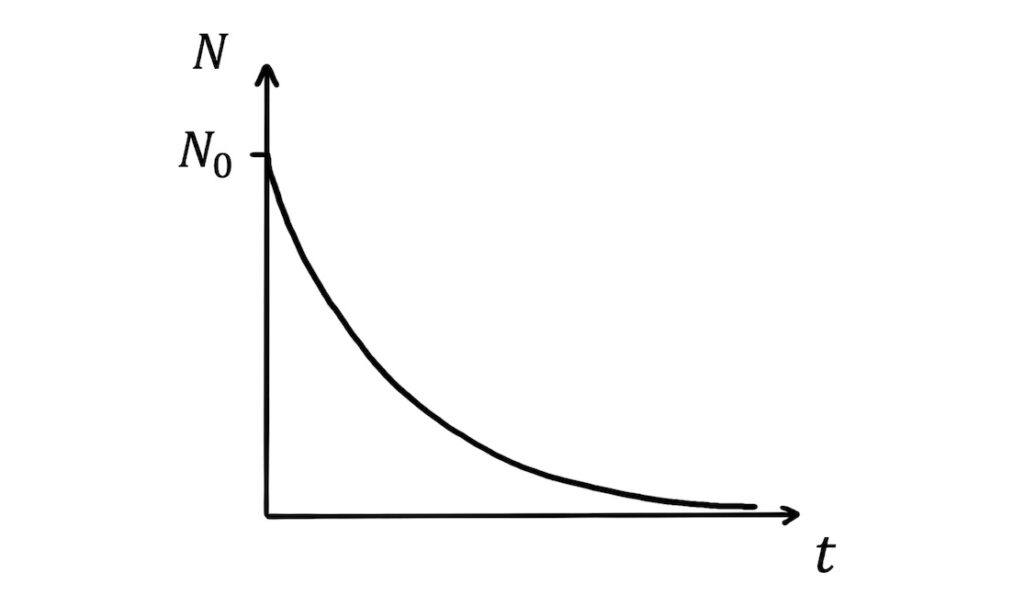
\(N=N_0e^{-\lambda t}\)
As you can see from the term \(e^{-\lambda t}\), the sample size decays exponentially with time:
We can also multiply the equation \(N=N_0e^{-\lambda t}\) by \(\lambda\) to get:
\(\lambda N=\lambda N_0e^{-\lambda t}\)
And since \(A=\lambda N\), we can write:
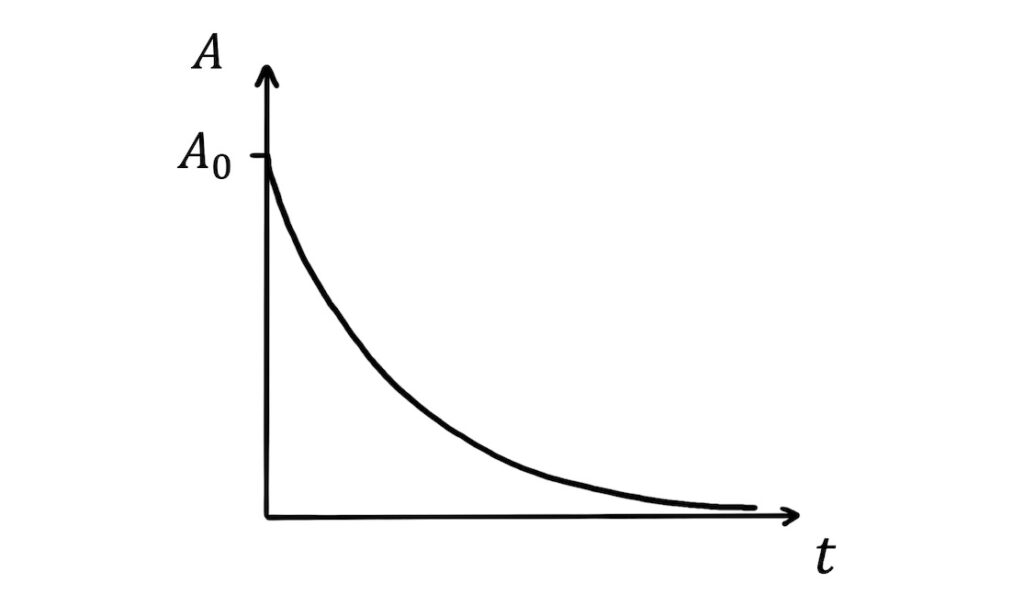
\(A=A_0e^{-\lambda t}\)
The activity of the sample therefore also decays exponentially with time:
How to calculate half-life
Half-life is a central concept in radioactivity. The half-life, \(t_{\frac{1}{2}}\), of a sample of nuclei is the time it takes for half the nuclei to decay:
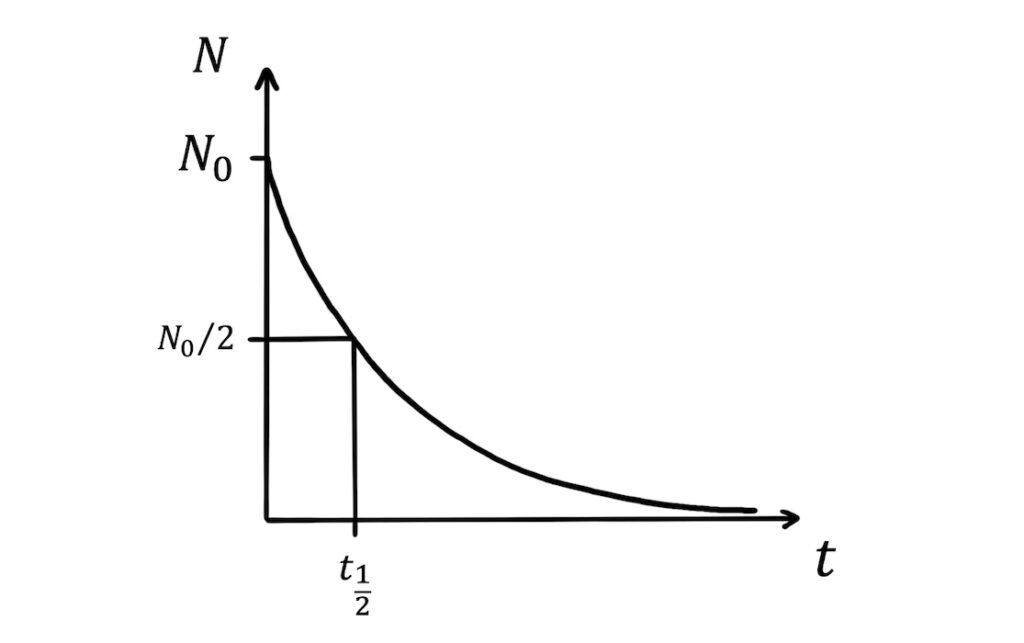
This means that when \(t=t_{\frac{1}{2}}\), \(N=\frac{N_0}{2}\). Substituting this into \(N=N_0e^{-\lambda t}\) gives:
\(\frac{N_0}{2}=N_0e^{-\lambda t_{\frac{1}{2}}}\)
Rearranging, we have:
\(-ln2=-\lambda t_{\frac{1}{2}}\)
And therefore we have the following expression for the half-life:
\(t_{\frac{1}{2}}=\frac{ln2}{\lambda}\)
Number of nuclei after a given number of half-lives
We can extend the concept of a half-life to consider what happens after any number of half-lives.
For example, after one half-life the sample is half its original size. After a second half-life, the sample halves again to become a quarter of its original size. After three half-lives, the sample is an eighth of its original size, and so on.
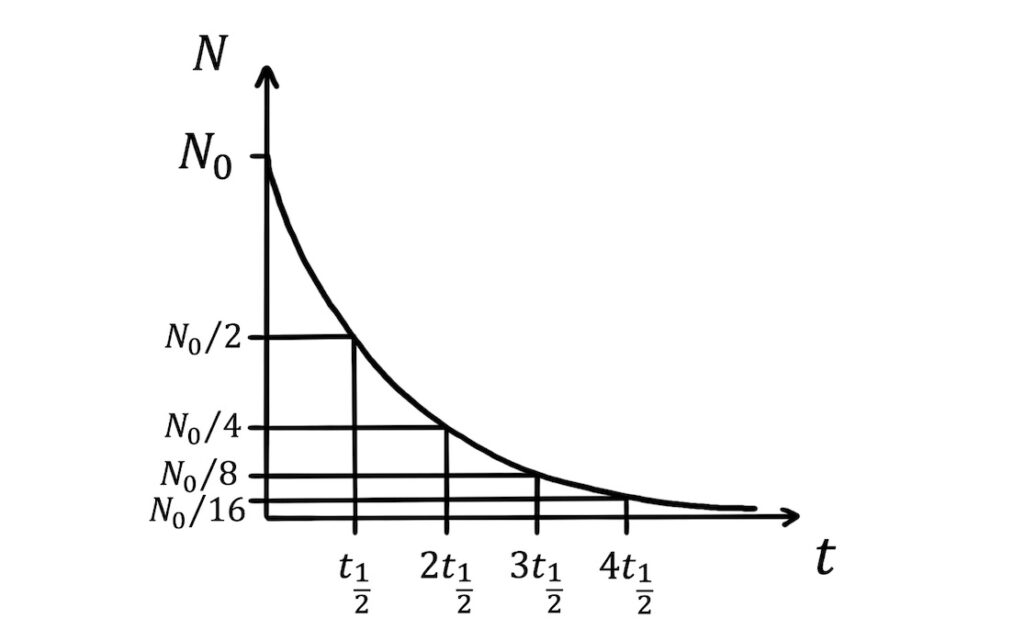
After \(x\) half-lives, \(t=xt_{\frac{1}{2}}\). Substituting this into \(N=N_0e^{-\lambda t}\) gives:
\(N=N_0e^{-\lambda (xt_{\frac{1}{2}})}\)
Let’s now use our expression for a half-life, \(t_{\frac{1}{2}}=\frac{ln2}{\lambda}\), to get:
\(N=N_0e^{-\lambda (x\frac{ln2}{\lambda})}\)
We can simplify this as follows:
\(N=N_0e^{-xln2}\)
\(=N_0e^{ln2^{-x}}\)
\(=N_02^{-x}\)
Therefore we can write:
\(N=\frac{N_0}{2^x}\)
This gives us an expression for the sample size, \(N\), after \(x\) half-lives, even if \(x\) is not a whole number!
Since \(A=\lambda N\), we can multiply this equation by \(\lambda\) to get a corresponding equation for the activity of a sample after \(x\) half-lives:
\(A=\frac{A_0}{2^x}\)
Conclusion
I hope you’ve enjoyed this review of the radioactive decay equations! How did you find the derivations? As you can see, with a few relatively simple bits of maths we can derive a powerful framework for describing radioactive decays which are random, probabilistic processes.
Armed with this strong foundational knowledge, you might like to explore in more detail the individual processes of alpha, beta and gamma decay.
Happy studying!
