Contents
Introduction
We use many of the same terms to describe standing waves and travelling waves, but in reality these waves are very different. Standing waves do not travel and, actually, they are just vibrations!
In this post we’re going to discover what standing waves are, how they are formed, and some of their principal characteristics.
Let’s begin!
What is a standing wave?
A standing wave, also known as a stationary wave, is the superposition of two travelling waves of the same frequency and amplitude travelling in opposite directions.
For example, consider two identical waves travelling towards each other. When they are in phase, they will constructively interfere to create a resultant wave of twice the amplitude!
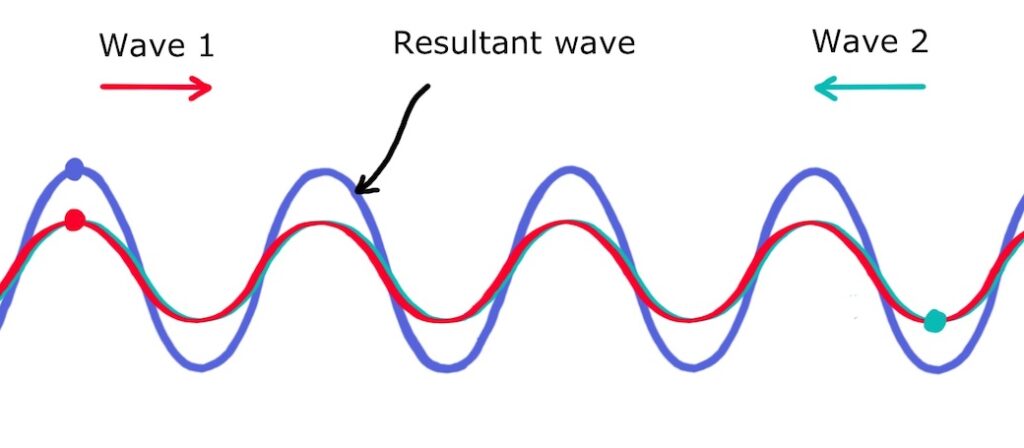
Let’s follow the red and green dots as the waves travel along. An eighth of a cycle later (\(t=T \big/ 8\)), the crests have moved along slightly and the resultant wave has a smaller amplitude:
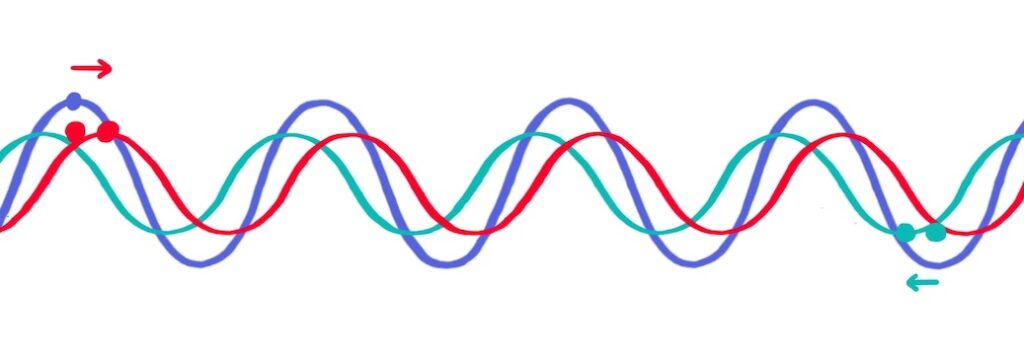
Another eighth of a cycle later (\(t=T \big/ 4\)), the crests have moved further along and the travelling waves are in antiphase. They deconstructively interfere and cancel each other out!
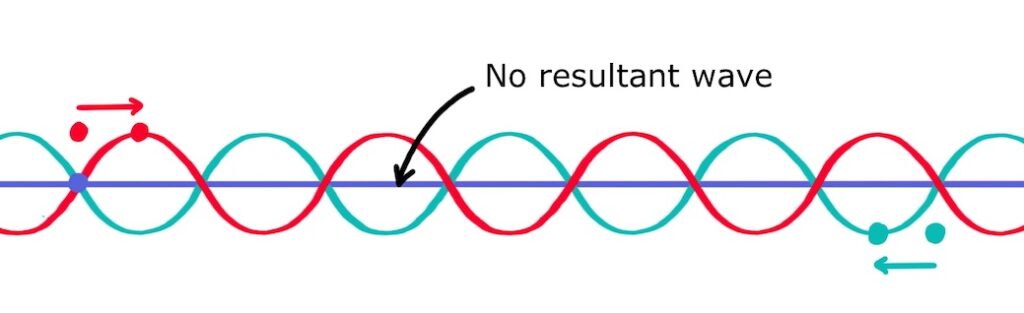
At \(t=3T \big/ 8\), the crests move a bit further and the standing wave reappears:

Finally, half way through the wave cycle (\(t=T \big/ 2\)), the travelling waves are in phase again. Each point on the standing wave has its maximum amplitude, but a negative version of what it had at the start.
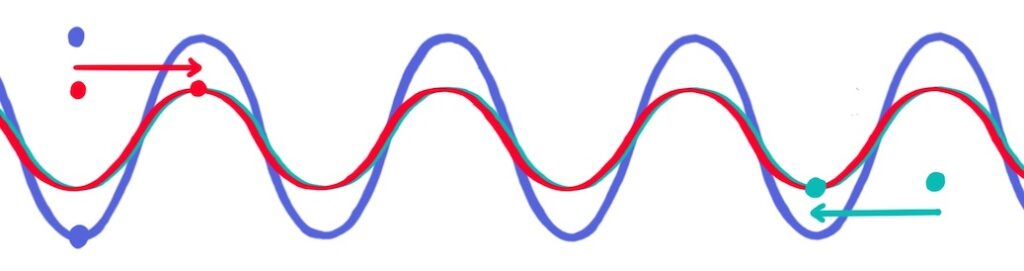
At this stage, the blue dot on the crest of the standing wave has moved from its starting position at the top all the way to the bottom:

During the next half cycle the blue dot moves all the way back up to the top. It is this repeating vibration that creates the standing wave:
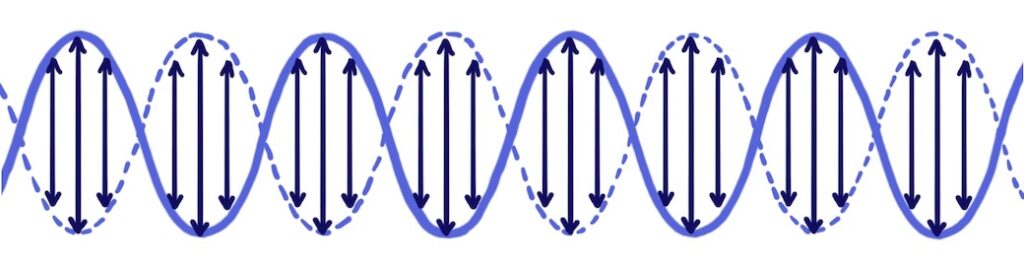
How standing waves are formed
A standing wave can be established in various ways.
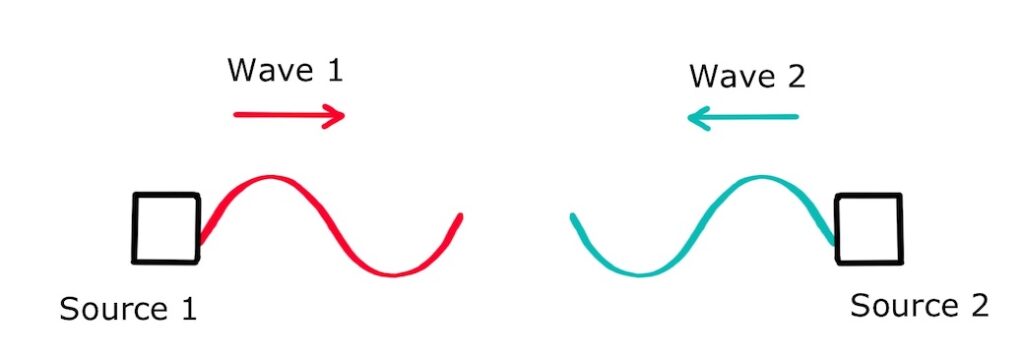
Two wave sources producing identical waves traveling towards each other can set up a standing wave:
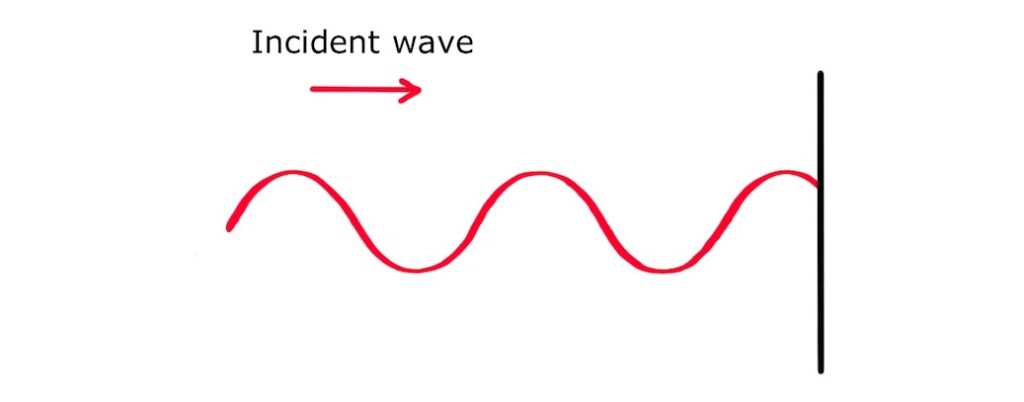
A standing wave can also be set up when a wave superimposes with its own reflection. For example, consider an incident wave meeting a boundary:
When it reflects, it changes direction and inverts:
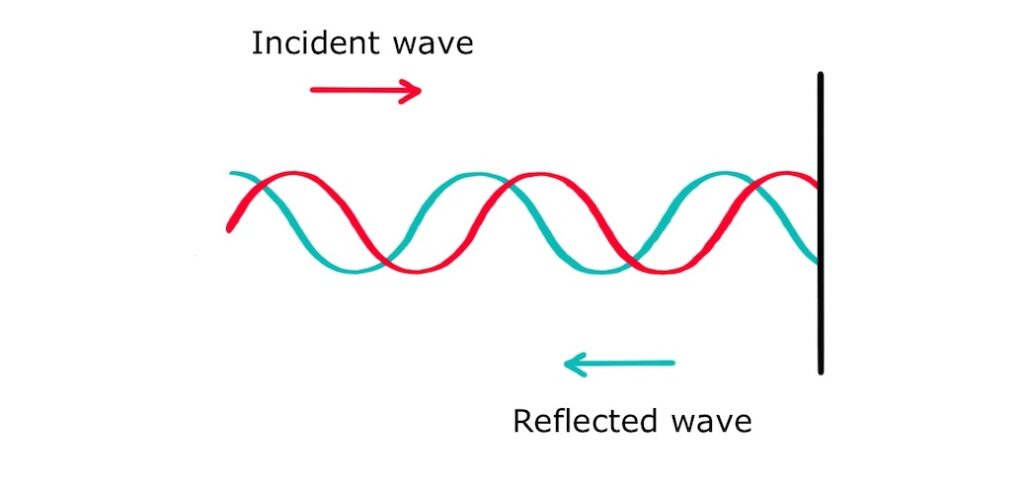
The resultant wave is a standing wave!
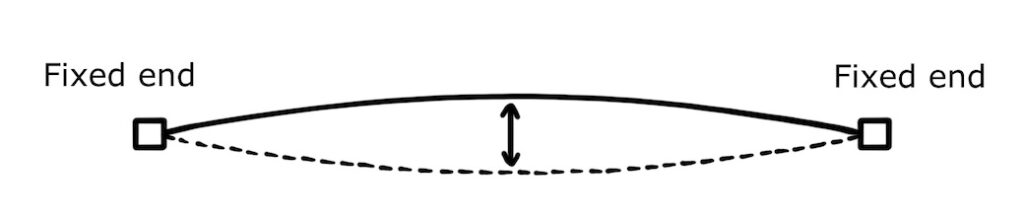
A standing wave can also be produced by plucking a string under tension:
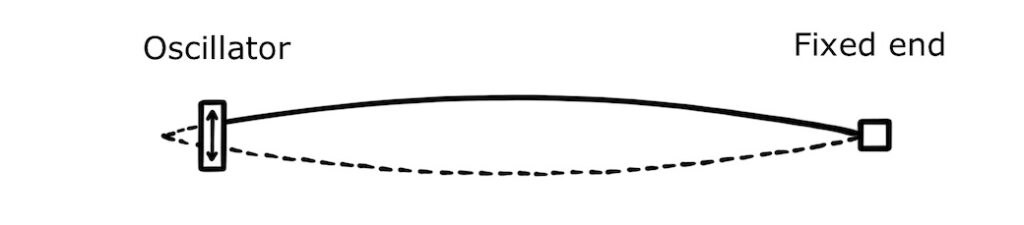
A similar way is to use an oscillator. At one end of the string, the oscillator vibrates to produce a travelling wave. This wave travels to the fixed end where it is reflected back, and if the oscillator completes a full cycle in the time it takes for the travelling wave to make a round trip, a standing wave is formed:
If the oscillator completes two cycles in this time, a higher frequency standing wave is formed:

It’s important that the oscillator completes a whole number of cycles in the time it takes for the travelling wave to do a round trip. If it doesn’t, the interference of the travelling wave and its reflection will create an irregular pattern, not a standing wave.
Harmonics on a string
Returning to the example of the plucked string, standing waves of various frequencies can be formed depending on where and how the string is plucked.
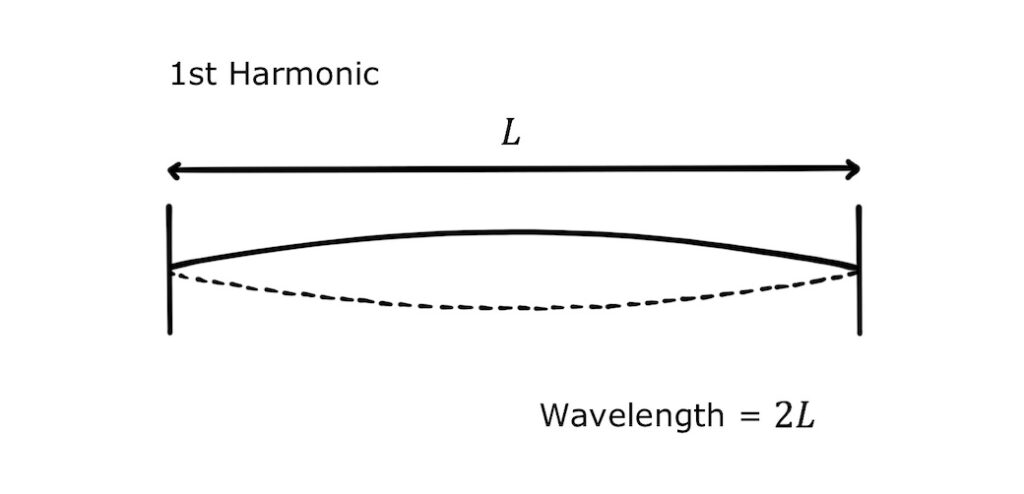
The example we saw above is the lowest frequency, called the first harmonic or fundamental mode. Its wavelength is twice the length of the string:
The second harmonic, also called the first overtone, has a wavelength that is the same length as the string. Since wave speed in the string is constant, the frequency is double that of the first harmonic (see the wave equation, below).
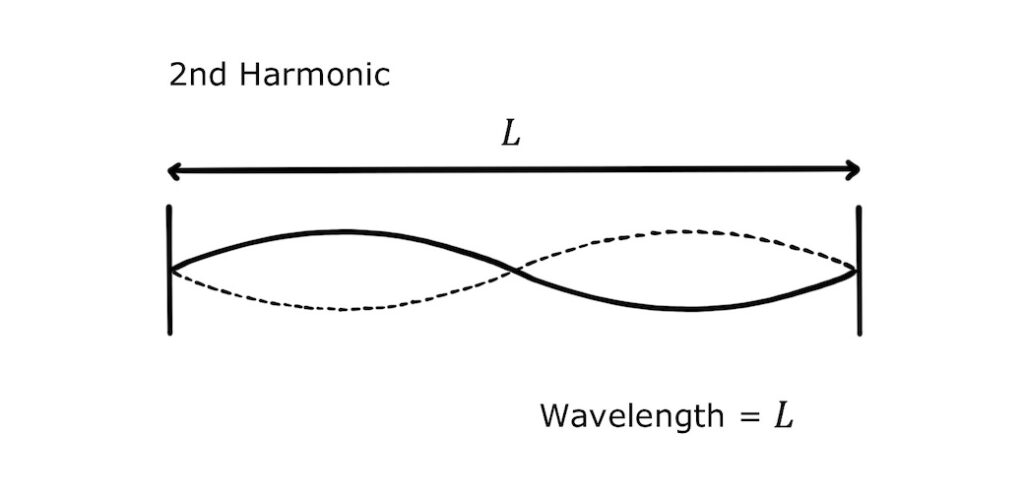
The third harmonic (second overtone) has a wavelength of two thirds of the length of the string:
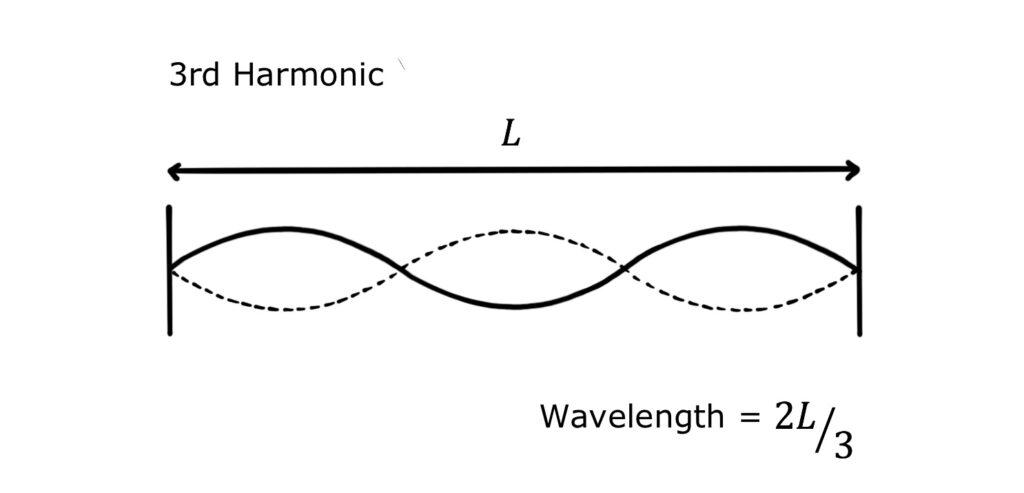
And the fourth harmonic (third overtone) has a wavelength of half the length of the string:
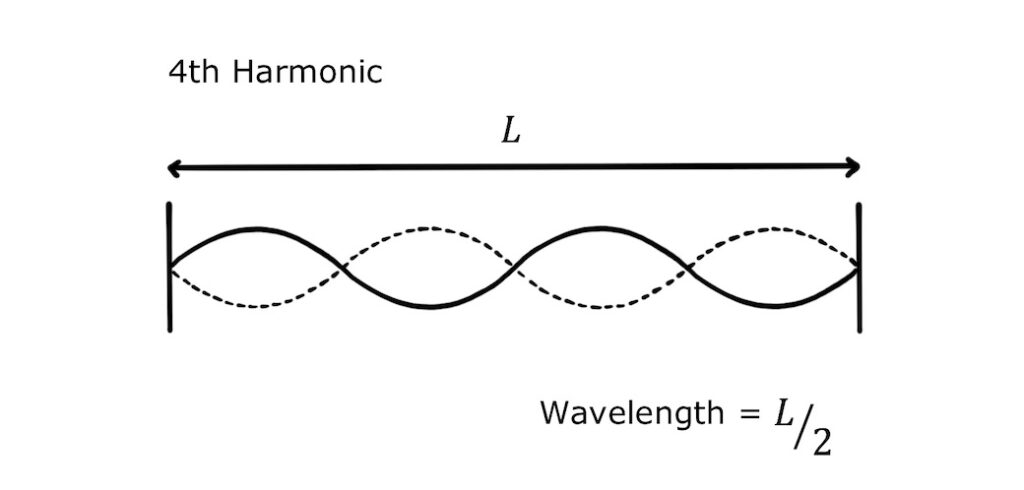
As you have probably guessed, there are infinite possible harmonics! Harmonics are important in music: for example, when stringed instruments are played, they vibrate with a combination of harmonics that give them their characteristic sounds.
Amplitude varies along a standing wave
Now that we’ve seen what standing waves are and how they can be formed, let’s review some of their principal characteristics!
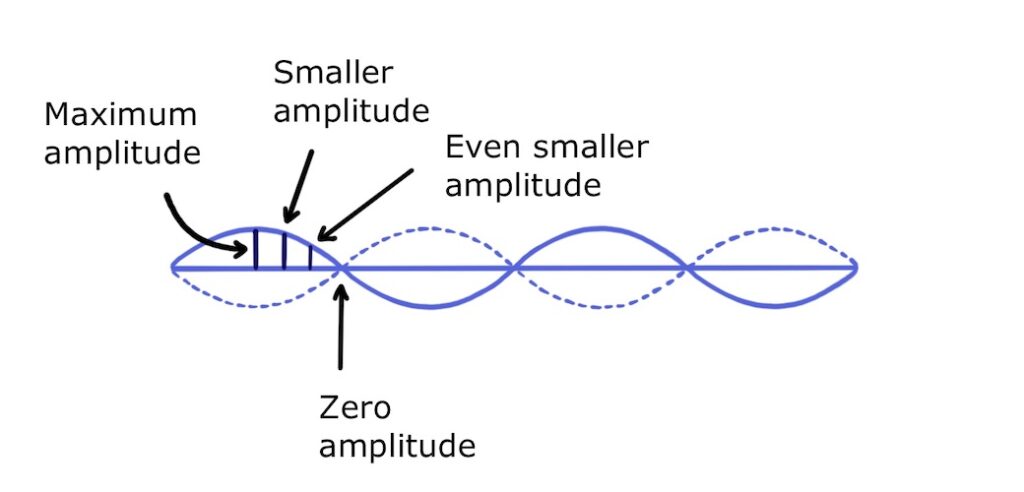
An important one is that, unlike travelling waves, the amplitude of a standing wave varies along the wave:
Nodes and antinodes
This lets us define some key terms. Points on a standing wave with zero amplitude are called nodes, and points with maximum amplitude are called antinodes:
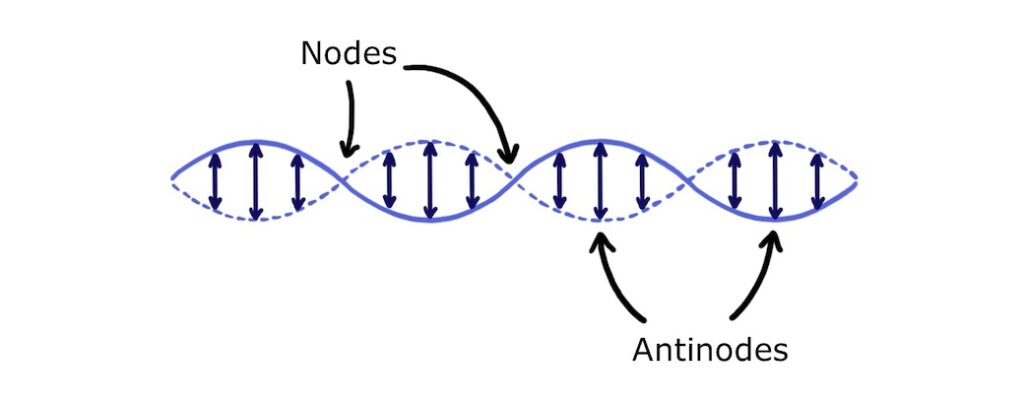
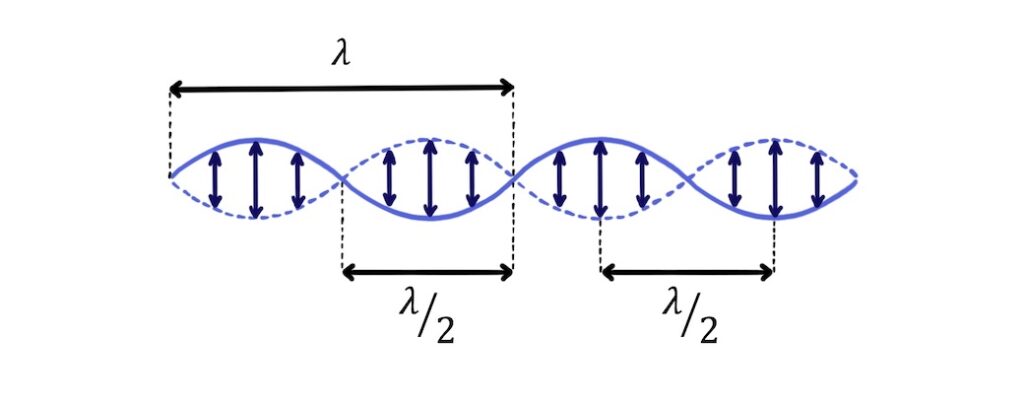
The distance between two adjacent nodes or between two adjacent antinodes is half a wavelength:
Phase difference in standing waves
The phase of a point on a standing wave is how far along its cycle it has reached.
For example, when points A, B and C are at the top of their cycle, points D, E and F are at the bottom of their cycle:
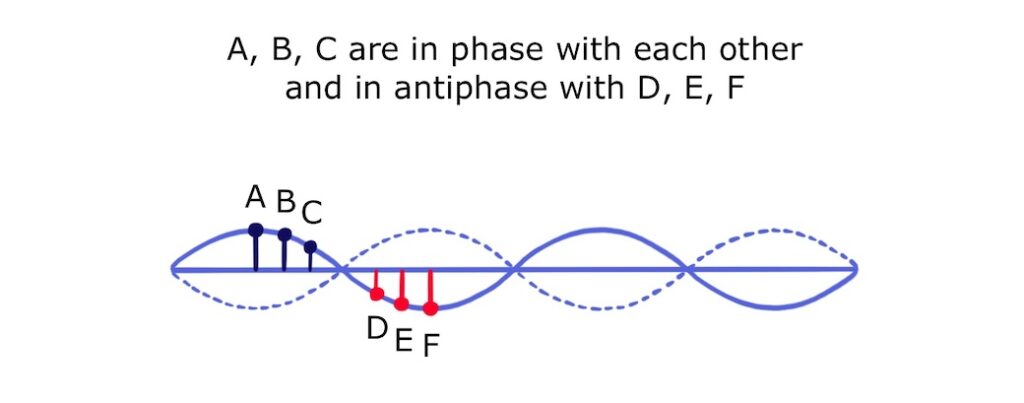
Points A, B and C are therefore in phase with each other but in antiphase with points D, E and F.
In more general terms, the points between adjacent nodes of a standing wave are in phase and the points either side of a node are in antiphase.
Speed of a standing wave
Even though standing waves do not travel, we can still use the wave equation to define their speed.
\(v=\lambda f\)
It might seem strange, but a standing wave has the same speed as the two travelling waves that interfered to create it because their wavelengths and frequencies are the same.
Standing waves store energy
Another important difference between travelling waves and standing waves is that while travelling waves transfer energy, standing waves store it.
To understand this, think of the identical travelling waves that travel towards each other to form a standing wave. They each carry the same energy but in opposite directions, so the net energy transfer is zero.
The energy has not disappeared though. It’s still in the system and is being stored by the standing wave.
Conclusion
I hope you’ve enjoyed learning about standing waves! They are very interesting phenomena, and differ from travelling waves in various key ways!
Why not learn more about their cousins, travelling waves, or explore in more detail the motion at each point on a standing or travelling wave by looking at the topic of simple harmonic motion?
Happy studying!
