Contents
Introduction
Early in the 20th century, the remarkable discovery was made that light could behave as a particle and that particles such as electrons could behave as waves. This flipped the traditional conceptualisation of these entities on its head, revealing that they had a dual nature and could behave as particles or waves depending on their circumstances.
In this post, we’re going to explore the quantum mechanical phenomenon of wave-particle duality and review the evidence that supports it.
Let’s begin!
What is wave-particle duality?
Wave-particle duality is the concept that waves can behave as particles and particles can behave as waves. Their behaviour at any given time depends on the prevailing experimental circumstances.
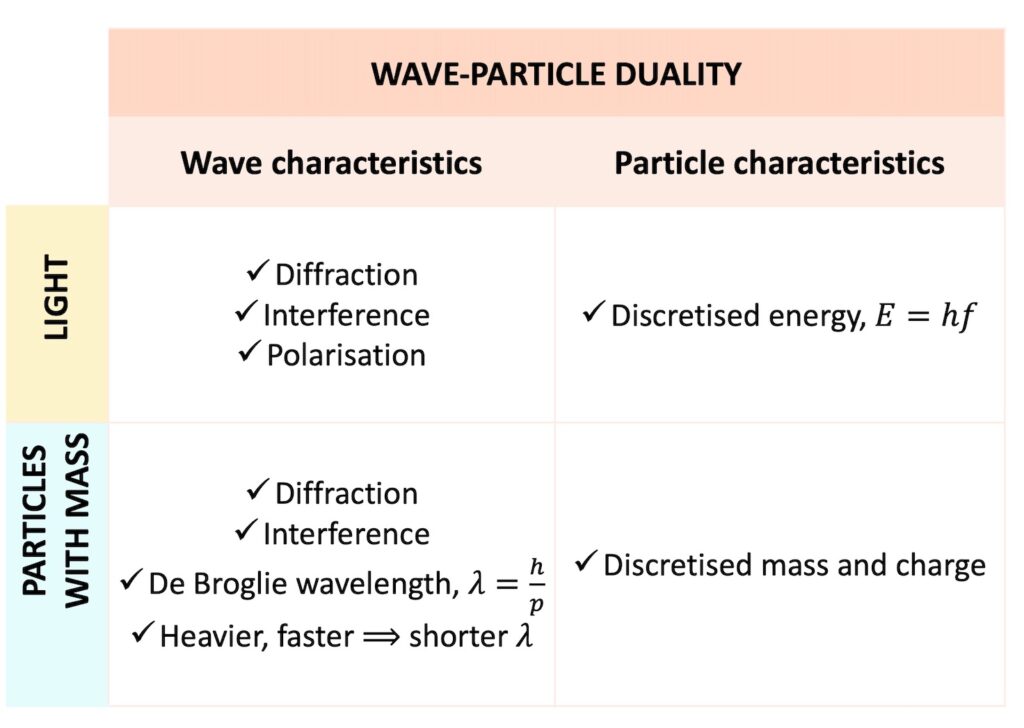
Thus, we can observe a single entity displaying wave characteristics such as diffraction, interference and polarisation at one time and particle characteristics such as a fixed mass and a fixed charge at another time.
Having a fixed, discrete amount of a property is sometimes referred to as discretisation. So we can say that an entity has discrete or discretised mass, charge, or energy.
Entities with wave-particle duality have both wave characteristics and particle characteristics as follows:
The dual nature of light
Before the early 20th century, light was thought of as a classical wave. Its wave-like behaviours of diffraction and interference were had been experimentally observed, but there was one experiment called the photoelectric effect that could not be explained by classical wave theory.
In this experiment, light was shone on a metal surface to give electrons in the metallic lattice some energy to escape. However, electrons were only liberated from the metal if the light’s frequency was at least a minimum threshold.
The minimum frequency required to liberate electrons from the metal surface could not be explained by classical wave theory. If light were purely a wave, then even with low frequencies it should be possible to give the electrons enough energy to escape by using a high enough intensity of light or by shining the light for long enough for the energy to accumulate. Neither of these worked!
To explain this, Einstein proposed in 1905 that light arrived in discrete packets of energy called photons (where each photon has energy \(E=hf\), where \(h\) is Plank’s constant and \(f\) is the frequency of the light). Photons, he proposed, were absorbed by electrons on a one-to-one basis. So if a photon had enough energy, it could help an electron escape. If it didn’t, the electron would stay in the metal.
This explained the minimum frequency requirement!
The photoelectric effect thus provides evidence of the particle nature of light, proving that light can behave as both a particle and a wave.
The dual nature of electrons
Nineteen years later, in 1924, the French physicist Louis de Broglie suggested that particles could behave like waves and have a wavelength. He proposed that a particle’s wavelength was inversely proportional to its momentum:
\(\lambda=\frac{h}{p}\)
The de Broglie wavelength was confirmed experimentally five years later by electron diffraction experiments. The basic setup is to accelerate electrons towards a crystal lattice which acts as a diffraction grating. Since the electrons can behave as waves, they diffract through the crystal lattice and create a diffraction pattern on a screen.
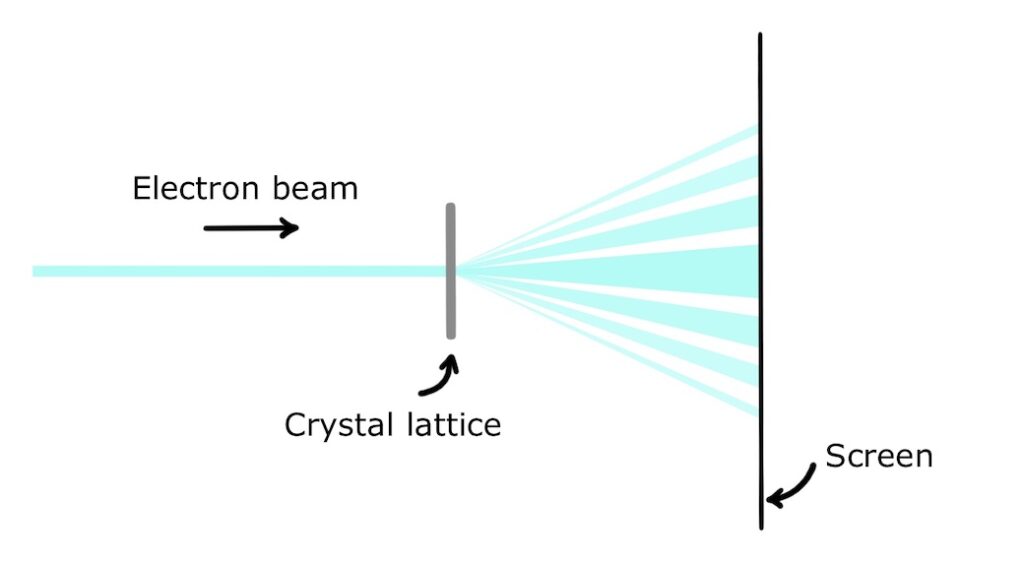
This experiment elegantly demonstrates both types of behaviour of electrons. While they are being accelerated towards the grating by an electric field, they exhibit their particle characteristics of fixed mass and charge. When they diffract through the grating, they exhibit their de Broglie wavelength. At the screen, they arrive at discrete locations, exhibiting their particle nature.
Since momentum is given by \(p=mv\), the faster the electrons travel, the shorter their wavelength. By adjusting the speed to which the electrons are accelerated, their de Broglie wavelength can be tuned to be approximately equal to the grating spacing so that diffraction can take place.
The dual nature of electrons is summarised as follows:
Wave nature of massive objects
We can expand this dual nature to other massive objects, not just electrons. Let’s look at some examples!
Since the de Broglie wavelength is \(\lambda=\frac{h}{p}=\frac{h}{mv}\), the greater an object’s mass, the shorter its wavelength. For example, an electron travelling at a speed of \(7.0\times 10^6\,\rm{ms^{-1}}\) has a de Broglie wavelength on the order of \(10^{-10}\,\rm{m}\). Meanwhile, a \(\rm{C}_{60}\) molecule (made of 60 carbon atoms) travelling at \(220\,\rm{ms^{-1}}\) has a wavelength on the order of \(10^{-12}\,\rm{m}\). Despite being slower, the heavy molecule has a much shorter wavelength than the tiny electron.
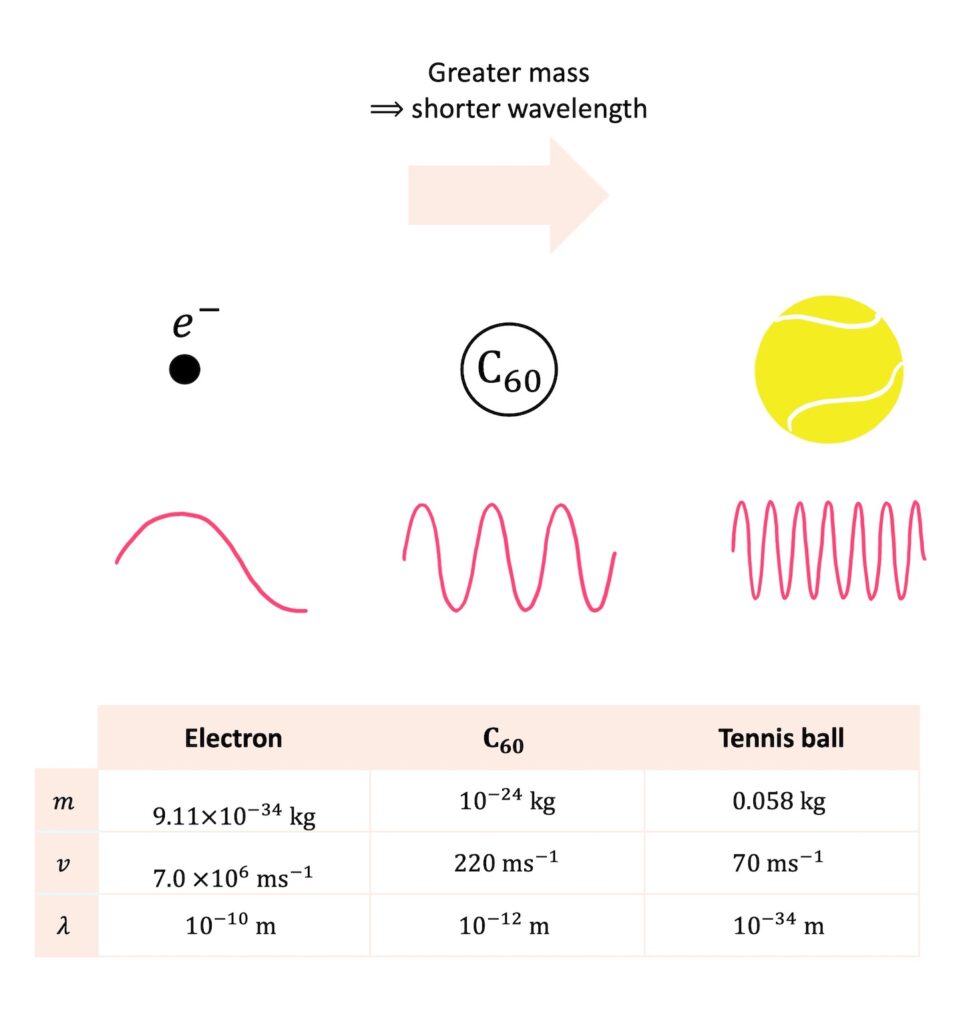
The wave nature of \(\rm{C}_{60}\) was demonstrated experimentally in a groundbreaking experiment in 1999. Although experimentally challenging, \(\rm{C}_{60}\) was shown to diffract through a crystal lattice, just like electrons. This provided powerful confirmation that wave-particle duality applies not only to subatomic particles, but also to significantly heavier objects.
What about a tennis ball?! A tennis ball travelling at \(70\,\rm{ms^{-1}}\) has a de Broglie wavelength on the order of \(10^{-34}\,\rm{m}\). This is absolutely minuscule! For comparison, the diameter of the nucleus of an atom is approximately \(10^{-15}\,\rm{m}\), so the tennis ball’s wavelength is \(10^{19}\) times smaller than the atomic nucleus.
The tennis ball’s wavelength is so small that there is nothing in the universe small enough for it to diffract through! As a result, we do not observe the wave-like characteristics of tennis balls and we only see them behaving as classical particles.
Summary
Here’s a handy summary of the key principles we’ve covered:
Conclusion
I hope you’ve enjoyed this review of wave-particle duality! We’ve explored the quantum mechanical principle of how light and massive particles such as electrons have a dual nature.
With these insights, you might enjoy taking a deeper dive into the fascinating topics of the photoelectric effect and electron diffraction.
Happy studying!